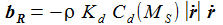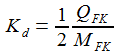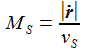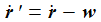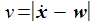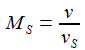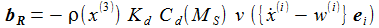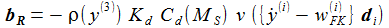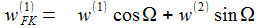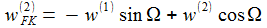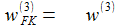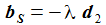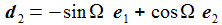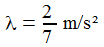|
|
Exkurs in die Ballistik mit SciLab |
|
|
|
|
|
|
... gepackt, zum Herunterladen. |
|
|
Etwas Geometrie
Die Ellipse
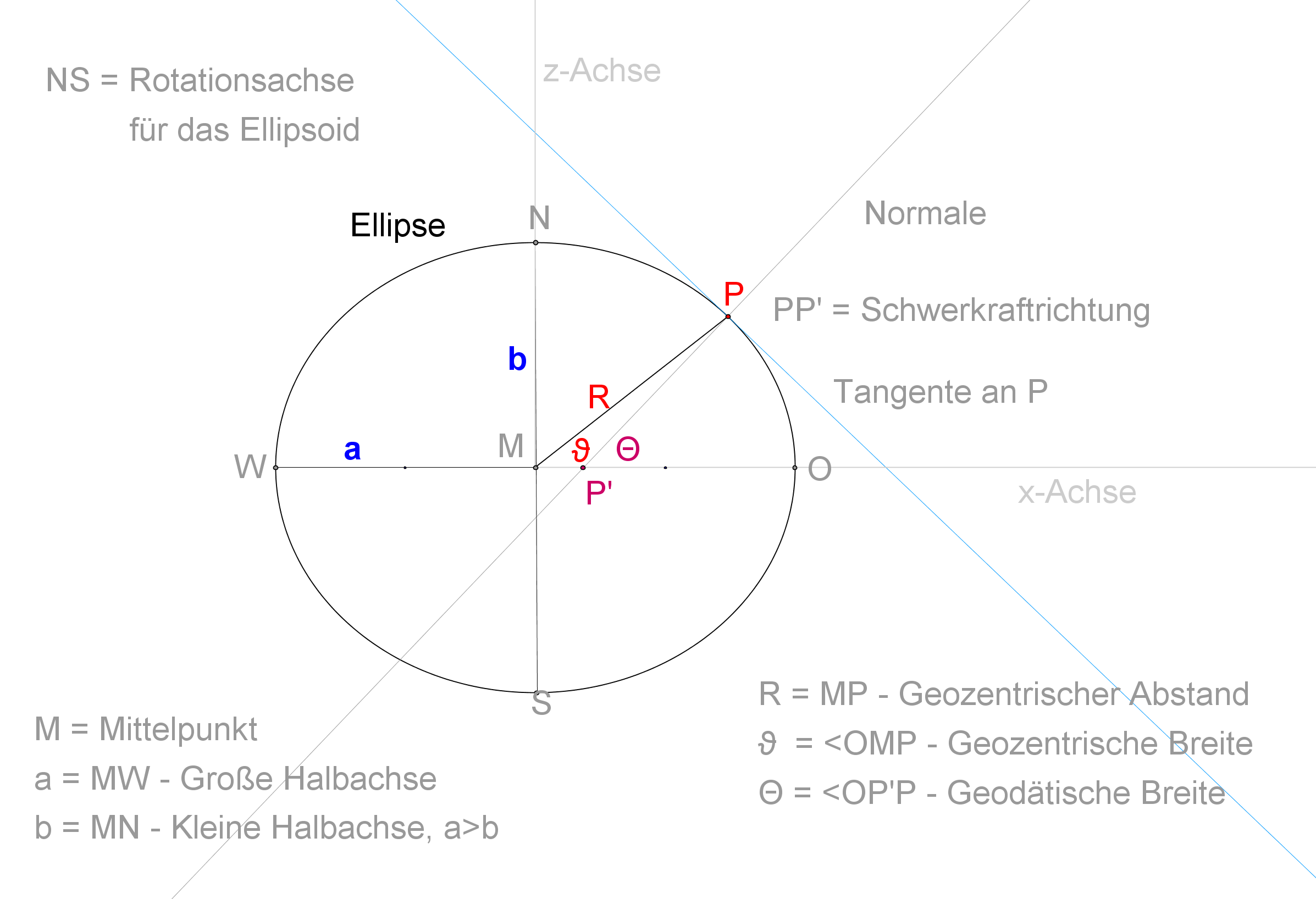
Ellipsenparameter
|
Die geodätische Breite (auch geografische Breite oder Breitengrad genannt) ist durch den Winkel Θ gegeben. Das mag überraschen, aber zu dieser Definition passt etwa, dass ein Seemann am Punkt P den Breitengrad seiner Position bestimmt, indem er mit dem Sextanten die Höhe des Polarsterns über 'seinen' Horizont misst – und dieser Horizont ist gerade durch die Tangentialebene an den Punkt P gegeben. |
|
Die Bestimungsstücke der Ellipse sind die beiden Halbachsen a und b. |
a > b |
|
Als Hilfsgrößen werden die Exzentrizität e und ε eingeführt. |
|
|
Einige einfache Zusammenhänge für diese Hilfsgrößen sind |
|
|
|
Das oblate Ellipsoid
|
Für die Halbachsen a und b des oblaten Ellipsoids gilt a>b. Ist das Ellipsoid dazu rotationssymmetrisch um die z-Achse, so erfüllen die kartesischen Koordinaten x,y,z eines Punktes P auf dem Ellipsoid die Gleichung: |
|
|
Die Parametrisierung der kartesischen Koordinaten x,y,z in sphärischen Polarkoordinaten R,ϑ,φ ist gegeben durch: |
|
|
|
|
|
Der Erdradius bezogen auf eine gegebene geodätische Breite Θ ist angenähert: |
|
|
|
Eigenschaften der Erde
Die Erdgestalt
|
Das WGS-84 Ellipsoid Der Radius des WGS-84 Ellipsoids nimmt also nach Norden um gut 21 km ab, das sind 0,34%. |
a = 6378137,0 m |
|
Die geozentrische und die geodätische Breite differieren höchstens um 0,2° und zwar in den mittleren Breitengraden, wie die folgende Grafik zeigt: |
|
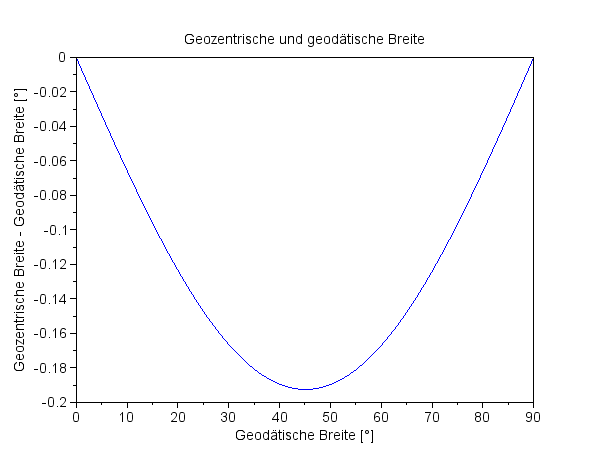
Differenz von geozentrischer und geodätischer Breite
| Oben wurde eine Formel für die Berechnung einer genäherten geozentrischen Breite ϑ~(1) aus der geodätischen Θ angegeben. Die folgende Grafik zeigt den Fehler der Näherung für die geozentrische Breite: |
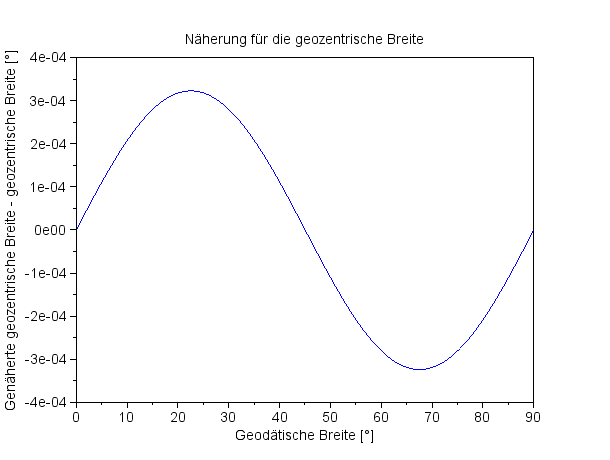
Fehler durch die Näherung der geozentrischen Beite
| In der folgenden Grafik ist der 'Erdradius' in Abhängigkeit von der geodätischen Breite dargestellt - 'Erdradius' meint hier den Radius des WGS-84 Ellipsoids: |
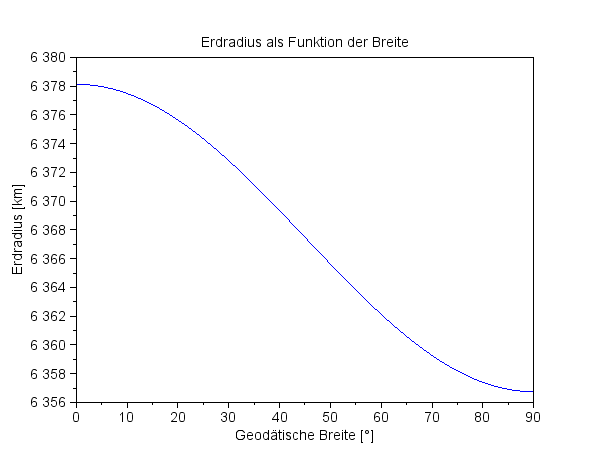
Erdradius als Funktion der geodätischen Breite
|
|
Die Koordinatensysteme
Das geozentrische Inertialsystem
|
Das Newtonsche Gesetz ist in einem Inertialsystem gültig. Solch ein rechtshändiges ruhendes Koordinatensystem ist mittels kartesischer Koordinaten wie folgt definiert: |
|
|
Das Koordinatensystem ist im Erdmittelpunkt PM befestigt, die x- und y-Achsen liegen in der Äquatorialsebene, zu einem bestimmten Zeitpunkt (hier t=0) zeigt die x-Achse in Richtung des Nullmeridians, die z-Achse zeigt nach Norden und markiert die Erdrotationsachse.
Ein Punkt P hat in diesem geozentrischen Inertialsystem
die kartesischen Koordinaten
|
|
|
Das geozentrische mitrotierende Bezugssystem
|
Ein fest an die Erde gebundenes, mitrotierendes rechtshändiges, Koordinatensystem Kf (f steht für fixiert) ist wie folgt definiert: In diesem Koordinatensystem sind die X(i) die kartesischen Koordinaten eines Punktes P. |
|
|
Dieses Koordinatensystem ist im Erdmittelpunkt PM befestigt, die X1- und X2-Achsen liegen in der Äquatorialsebene, die X1-Achse zeigt in Richtung des Nullmeridians, die X3-Achse zeigt nach Norden und markiert die Erdrotationsachse. |
|
Die beiden Koordinatensysteme
Die Matrix D~3(ωt) beschreibt eine Drehung gegen den Uhrzeigersinn um die X3-Achse mit dem Winkel ωt. |
|
|
Ausgeschrieben wird das für die drei Basisvektoren E(i) zu: |
|
|
|
Das ENU-Beobachter-Koordinatensystem
|
Das kartesische ENU-Koordinatensystem KB eines Beobachters B ist wie folgt definiert: Es ist am Standort PB(φB, ϑB, hB) des Beobachters befestigt, die x1- und x2-Achsen liegen in der Tangentialebene durch den Punkt PB, die x1-Achse (East) zeigt nach Osten, die x2-Achse (North) zeigt nach Norden, die x3-Achse (Up) zeigt in Richtung Zenit (also weg vom Erdmittelpunkt). hB ist etwa die Höhe des Beobachters über dem Ellipsoid, bei Bedarf auch die über dem Meeresspiegel. |
|
|
Im Folgenden führt die Matrix D~i(α) eine Drehung gegen den Uhrzeigersinn um die i-Achse des Koordinatensystems mit dem Winkel α aus. |
|
|
|
|
Das Koordinatensystem des Beobachters KB
ist mit den geozentrischen
Koordinatensystemen
Die orthogonale Matrix P~ permutiert einfach die Koordinatenachsen, diese Permutation der Achsen entspricht einer Drehung um die Achse (1,1,1). Beachte: Die beiden Winkel ϑ und φ sind die Winkel ϑB und φB des Beobachtungsstandortes, der Index B wurde und wird im Folgenden weggelassen. Die Matrix D~E e überführt die drei Basisvektoren E(k) des geozentrischen, mitrotierenden Bezugssystems in die drei Basisvektoren e(k) des ENU-Bezugsystems des Beobachters. |
|
|
In Komponenten ausgeschrieben sieht die Matrix D~E e und die inverse Matrix D~e E wie folgt aus: |
|
|
|
Die Matrix D~E- e überführt die drei Basisvektoren E-(k) des geozentrischen Inertialsystems in die drei Basisvektoren e(k) des ENU-Bezugsystems des Beobachters. |
|
|
In Komponenten ausgeschrieben sieht die Matrix D~E- e wie folgt aus: |
|
|
|
Die Basisvektoren {ei} des ENU-Bezugssystems im Punkt P(ϑ,φ) bilden ein rechtshändiges Dreibein mit den kartesischen Koordinaten: Die Koordinaten beziehen sich auf das geozentrische, mitrotierende Koordinatensystem Kf mit der Basis {Ei}. ϑ und φ sind die sphärischen Winkelkoordinaten des Punktes P im Koordinatensystem Kf. Der Vektor e1 zeigt nach Osten; der Vektor e2 zeigt nach Norden. Der Vektor e3 zeigt in Richtung der Erdachse. |
|
|
Einige nützliche Rechenhilfen: |
|
|
|
|
|
|
Das DCU-Flugkörper-Koordinatensystem
|
Das Flugkörpersystem KFK wird so gewählt, dass seine Koordinaten zur Beschreibung einer ballistischen Flugbahn 'bestens' geeignet sind – und eine ballistische Flugbahn liegt »mit kleinen Abweichungen« in einer Ebene, der Flugbahnebene. Das rechtshändige Koordinatensystem KFK ist wie folgt definiert: |
|
|
Das Flugkörpersystem KFK ist in einem gewählten Punkt PO auf der anfänglichen Flugbahn befestigt, die beiden Vektoren d1 und d2 spannen die Tangentialebene senkrecht zur Flugbahnebene auf, d1 liegt in der Flugbahnebene und zeigt in Flugrichtung, d2 steht senkrecht auf der Flugbahnebene und d3 zeigt wie e3 in Richtung der 'Erdachse'. hO ist etwa die Höhe des Flugbahnpunktes über dem Ellipsoid. 'DCU' steht für 'Down-range', 'Cross-plane', 'Up'. |
|
|
Einige nützliche Zusammenhänge: |
|
|
|
|
|
|
|
|
Das Beobachtersystem und das Flugkörpersystem sind durch eine Translation
|
|
Für ein Punkt P sind dessen Ortskoordinaten {xi} im Beobachtersystem mit den Koordinaten im Flugkörpersystem {yi} wie folgt verknüpft:
|
|
|
Für ein Punkt P sind dessen Geschwindigkeitskoordinaten im Beobachtersystem mit den Geschwindigkeitskoordinaten im Flugkörpersystem wie folgt verknüpft:
|
|
|
Für meine Zwecke ergibt sich der Winkel ΩBO einfach aus den als bekannt vorausgesetzten Größen Abschussgeschwindigkeit und Abschussrichtung des Flugkörpers, beides wird in dem Vektor v0 zusammengefasst; die Komponenten des Vektor v0 werden im Beobachtersystem (ENU) mit v0(i) bezeichnet:
|
|
|
|
Eigenschaften der Erde
Die Schwerkraftbeschleunigung
|
Ein Körper mit der Masse m erfährt im Schwerefeld der Erde am Ort P eine negative Beschleunigung bG senkrecht zur Tangentialebene an der Äquipotentialfläche des Schwerefeldes. |
|
|
Hier wird [ohne weiteres Nachdenken, weil für meine Zwecke ausreichend] die Näherung verwendet, dass das Schwerefeld rotationssymmetrisch, also nur vom Breitengrad des Punktes abhängig ist, und zusätzlich, dass die Schwerkraft radial zum Erdmittelpunkt wirkt. Die Gravitationskonstante ist also in Maßen ortsabhängig. |
|
|
Die Schwerkraft, die real im Experiment auf der Erde gemessen wird, ist die Resultierende aus der Gravitationskraft, die aufgrund der Erdanziehung auf den Körper einwirkt, und aus der ihr entgegengesetzten Zentrifugalkraft, die aufgrund der Erdrotation auf den Körper einwirkt. Der nicht-inertiale Schwerebeschleunigungvektor bG schließt hier die die gesamte Beschleunigung in radialer Richtung ein. |
|
Der Beobachterstandort PB hat die geodätische Breite θB und die Höhe hB über den Meeresspiegel (NN). g45 ist die Erdbeschleunigung am Breitengrad 45° auf Meereshöhe. Die Erdbescheunigung gB am Beobachtungsstandort ist dann 'in einem universellen Modell' gegeben durch: |
|
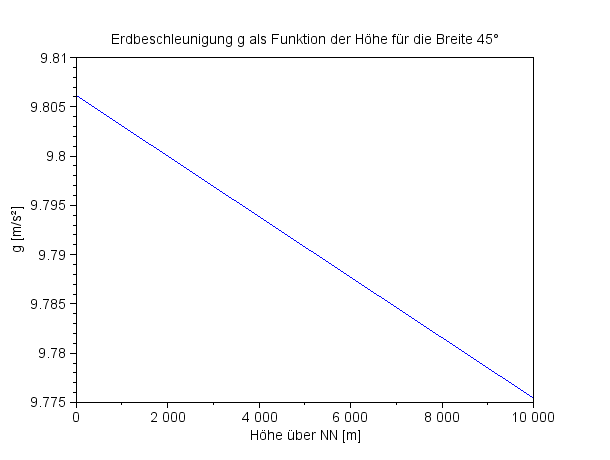
Die Erdbeschleunigung für die geodätische Breite 45°
und den Höhenmeterbereich 0 ... 10 000 m.
|
In 10 Kilometer Höhe hat in diesem Modell die Schwerebeschleunigung um 0,31% abgenommen. |
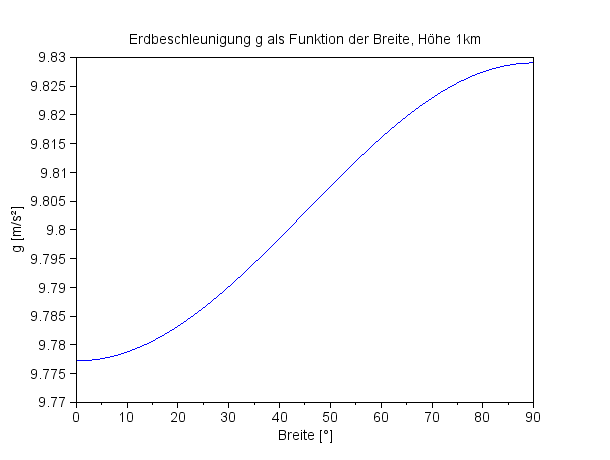
Die Erdbeschleunigung abhängig von der Breite für die Höhe 1 km
|
Auf dem Weg zum Nordpol nimmt die Schwerebeschleunigung um 0,53 % zu, entsprehend wie der Erdradius durch die abgeplattete Erdgestalt kürzer wird. |
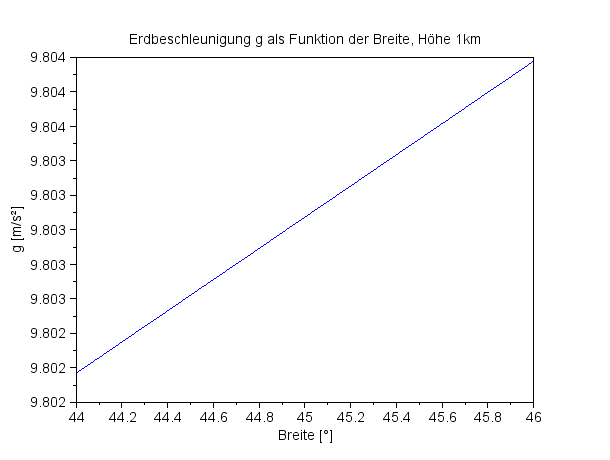
Die Erdbeschleunigung in einem Streifen von 2° um die Breite 45°
|
In einem Streifen von 2° etwa um den Breitengrad von 45° nimmt die Erdbeschleunigung nur um 0,018% ab. Dieser Streifen hat eine Breite von rund 225 km. Über solche Entfernungen kann die Erdbeschleunigung als konstant in der Breite angenommen werden. |
|
|
Die Schallgeschwindigkeit
|
Die Schallgeschwindigkeit in der Höhe h über den Meeresiegel ist in einem universellen Modell: |
|
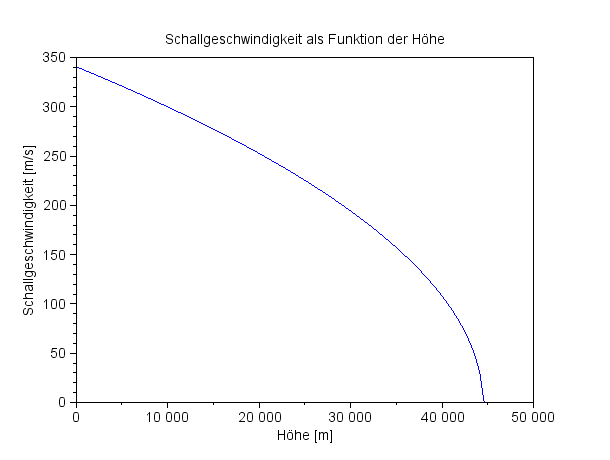
Die Schallgeschwindigkeit abhängig von der Höhe
|
|
Die Luftdichte
|
Die Dichte der Luft in der Höhe h über dem Meeresspiegel (NN) ist in einem universellen Modell: ρ0 ist die Luftdichte bezogen auf NN, Ha ist ein Skalenfaktor. |
|
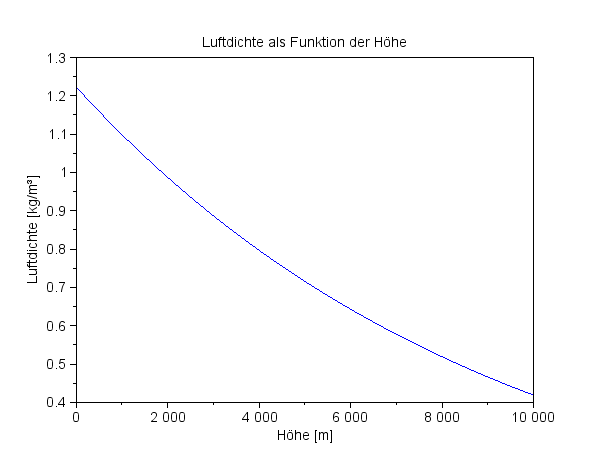
Die Luftdichte abhängig von der Höhe
|
In 10 km Höhe hat die Luftdichte auf ein Drittel des Wertes auf Meereshöhe abgenommen. |
|
|
Die Scheinkräfte
|
Dreht sich ein Körper, hier also die Erde, mit der konstanten
Winkelgeschwindigkeit ω
um die z-Achse, so hängen die Koordinaten
|
|
|
Ein Punkt P ruhe im mitbewegten System Kf. Mit einer kleinen (infinitisemalen) Zeitänderung δt erhält man die nebenstehenden Änderungen der Komponenten des Punktes - also die Geschwindigkeitskomponenten - im Inertialsystem: |
|
|
Betrachtet man eine allgemeine Rotation mit den drei Winkelgeschwindigkeiten ω(j) jeweils um die j-Achse, so verallgemeinern sich Änderungen der Komponenten des Punktes zu: εijk ist das vollständig antisymmetrische Levi-Civita-Symbol. |
|
|
Hat der Punkt P noch eine nicht weiter eingeschränkte Eigenbewegung relativ zum mitbewegten System, so ergibt sich: |
|
|
Führt man den axialen Rotationvektor ω und das Vektorprodukt ein, so lassen sich die Komponentengleichungen vektoriell zusammenfassen: Die Variation des Ortes eines Punktes in der Zeit definiert den inertialen Geschwindigkeitsvektor v: |
|
|
Die Variation der Geschwindigkeit eines Punktes in der Zeit definiert den inertialen Beschleunigungsvektor b: |
|
|
|
|
Das ergibt die Coriolisbeschleunigung bC und die Zentripetalbeschleunigung bZ: |
|
|
|
Die Coriolisbeschleunigung
|
Die Corioliskraft KC = m bC wirkt senkrecht zur (aktuellen) Rotationsachse und wirkt zudem senkrecht zum Geschwindigkeitsvektor eines bewegten Körpers der Masse m und führt damit zu einer zusätzlichen transversalen Bewegung des Körpers. |
|
|
Ein Beispiel: Fliegt ein Körper mit der Geschwindigkeit 300 m/s (1080 km/h), so ergibt sich eine Coriolisbeschleunigung von maximal 0,022 m/s², das sind zwar nur Bruchteile der Gravitationsbeschleunigung (0,22%). Allerdings hat diese Coriolisbeschleunigung diese ganz andere, ablenkende Wirkung senkrecht zur eigentlichen Bewegungsrichtung, was ihrer Wirkung eine neue Qualität verleiht, man schaue sich ihre Wirkung etwa in der Erdatmospäre an. Bläst der Wind etwa stetig in Ostrichtung, so wirkt die Coriolisbeschleunigung in Richtung Norden, der anfängliche Ostwind wird auf seinem Weg nach Osten nach und nach und immer mehr in die nördliche Richtung abgelenkt. Die erstaunliche Corioliskraft bewirkt also eine großräumige Windablenkung und hat damit eine gestaltende Kraft in der Erdatmospäre. |
|
Im ENU-Beobachtersystem KB(θB) erhält man für die Coriolisbeschleunigung die kartesischen Komponenten (θ=θB): |
|
|
Am Nordpol ist θB=π/2: |
|
|
Am Äquator ist θB=0: |
|
|
Im DCU-Flugkörper-Bezugssystem KFK erhält man für die kartesischen Komponenten der Coriolisbeschleunigung:
|
|
|
Einen sehr schönen Nachweis der Erdrotation im Kleinen lässt sich mit dem Foucault’schen Pendel aufzeigen. Ein solches ist etwa im deutschen Museum in München zu besichtigen. Das Pendel scheint zunächst einfach nur in einer Ebene hin und her zu schwingen; wartet man allerdings eine kleine Zeit, so sieht man, das die Schwingungsebene sich langsam um die vertikale Achse dreht. Markierungen am Boden helfen, die Gewissheit zu unterstützen. Für den Beobachter sieht es so aus, als gäbe es eine Kraft senkrecht zur Schwingungsebene des Pendels, die zu einem Drehmoment führt, welches die Drehung der Schwingungsebene bewirkt; diese scheinbar wirkende Kraft ist eben die Corioliskraft – eine sogenannte Scheinkraft, denn nicht die Schwingungsebene des Pendels dreht sich, wie es für den Beobachter den Anschein hat, sondern es dreht sich der Boden unter dem Pendel. Man kann sich diesen Umstand gut verdeutlichen, wenn man das Pendel gedanklich (oder auch tatsächlich) am Nordpol schwingen lässt: Die Erde muss sich offensichtlich in 24 Stunden einmal unter dem Pendel hinweg drehen mitsamt dem auf der Erde stehenden Beobachter. Erst ein Beobachter, der aus dem Weltraum das Treiben am Nordpol beobachtet, würde zweifelsfrei feststellen, dass sich die Erde dreht und dass das Pendel seine ursprüngliche Schwingungsrichtung beibehält. Nun fällt es auch nicht mehr schwer, abzuschätzen, wie lange in etwa ein Beobachter warten muss, bis er sein Heureka über den Erfolg des Experiments ausstoßen darf. Der Namensgeber des Pendels „Foucault verwendete einen schweren Pendelkörper von 28 Kilogramm, der an einem 67 Meter langen, dünnen Draht aufgehängt war. Das hohe Gewicht des Pendelkörpers stabilisierte die Pendelbewegung und machte sie dadurch weniger anfällig gegen Störungen durch Luftströmungen oder Verdrillung des Drahts. Die Länge des Pendels hingegen ermöglichte eine große Schwingungsperiode (16,5 Sekunden) und lieferte einen relativ großen Pendelausschlag. Innerhalb einer Stunde wich die Schwingungsebene um ungefähr elf Grad von der ursprünglichen Richtung ab.“ (Antje Harder, Microsoft Encarta 2002) |
|
Zurück zu den fliegenden Wurfgeschossen:
|
|
Für die Flugbahn wurden folgende Parameter im ENU-Bezugssystem verwendet:
Kd=5,6E-04; ('Drag') lambda=2,0/7,0; ('Lift') |
Geodätische Breite=52°; Beobachterstandort/Anfangsort=(100, 0, 0); Richtwinkel(QE)=45°; Azimuth(OM)=90°; Anfangsgeschwindigkeit(MV)=330; [m/s] MVx=MV*cos(QE)*cos(OM); MVy=MV*cos(QE)*sin(OM); MVz=MV*sin(QE)); Anfangsgeschwindigkeit=(MVx, MVy, MVz); |
|
Mit der Corioliskraft ... |
Ohne der Corioliskraft ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel : 45 Omega (Azimuth) : 90 Winddaten ENU : 0,0 | 0,0 | 0,0 ===> größte Höhe : 2406,7 Aufschlagszeit : 44,3384 Aufschlagsort DCU : 8803,8 | 16,0 | 0,0 Aufschlagsort ENU : 84,0 | 8803,8 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel : 45 Omega (Azimuth) : 90 Winddaten ENU : 0,0 | 0,0 | 0,0 ===> größte Höhe : 2406,7 Aufschlagszeit : 44,3385 Aufschlagsort DCU : 8803,8 | 0,1 | 0,0 Aufschlagsort ENU : 99,9 | 8803,8 | 0,0 |
|
|
Die Zentripetalbeschleunigung
|
Ein beliebiger Punkt P habe im mitbewegten lokalen Bezugssystem KB (ENU), welches im Punkt PB befestigt ist und das die Basis {ei} hat, die Koordinaten {xi}, dann gilt : |
|
|
|
|
Im ersten additiven Term von bZ geht der Abstand des Punktes PB vom Erdmittelpunkt ein, also im wesentlichen der Erdradius. In den zweiten Term geht dagegen nur der Abstand des Flugkörpers vom Nullpunkt des Bezugssystems KB ein. Wenn man den räumlichen Bereich für den Flugkörper auf 100 km ansetzt, ist dieser zweite Term gegenüber dem ersten zu vernachlässigen. |
|
Das doppelte Kreuzprodukt wird in 2 additive Terme aufgelöst. Der zweite Term (ω2 tMB) wirkt in radialer Richtung, in der auch die Schwerkraft wirkt. Dieser radiale Term geht diekt in das hier verwendete Schwerkraftmodell mit experimentell ermittelten Schwerkraftdaten auf und wird hier deshalb unterdrückt. |
|
|
Im Beobachtersystem KB (ENU) erhält man für die Zentripetalbeschleunigung die nebenstehenden kartesischen Komponenten, wobei die Komponente in radialer z-Richtung (~ e3) von der verwendeten Gravitationsbeschleunigung absorbiert wird und deshlb hier zu 0 gesetzt wird: |
|
|
Im Flugkörper-Bezugssystem (DCU) ergibt sich für die nicht-radialen Komponenten:
|
|
|
Zum Vergleichen: |
|
Ohne dem Zentripetalbeschleunigungsterm ... |
Mit dem Zentripetalbeschleunigungterm ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel : 45 Omega (Azimuth) : 90 Winddaten ENU : 0,0 | 0,0 | 0,0 ===> größte Höhe : 2406,8 Aufschlagszeit : 44,3387 Aufschlagsort DCU : 8790,1 | 15,9 | 0,0 Aufschlagsort ENU : 84,1 | 8790,1 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel : 45 Omega (Azimuth) : 90 Winddaten ENU : 0,0 | 0,0 | 0,0 ===> größte Höhe : 2406,7 Aufschlagszeit: 44,3384 Aufschlagsort DCU : 8803,8 | 16,0 | 0,0 Aufschlagsort ENU : 84,0 | 8803,8 | 0,0 |
|
|
Die wirksamen Kräfte
Die Schwerkraftskomponenten
|
Die Komponenten des Beschleunigungsvektor bG(P) am Ort P des Flugkörpers ergeben sich wie folgt, wobei die folgenden Größen verwendet werden: |
|
||||||
|
PB ist der Beobachterstandort und hP die dazugehörige Höhe des Beobachters über den Meeresspiegel. hP ist die Höhe des Flugkörpers über den Meeresspiegel. |
|||||||
|
Für den Beschleunigungsvektor bG(P) über der Flugbahn wird vereinfachend angesetzt, dass er in Richtung des Erdmittelpunktes weist. |
|
||||||
|
Zudem wird über die Flugbahn die Abhängigkeit des Beschleunigungsvektors von der geodätischen Breite vernachlässigt. Es verbleibt für gP=g(P) die quadratisch inverse Abhängigkeit vom Erdabstand |RP|: |
|
||||||
|
Mit diesen Näherungen lässt sich die Stärke des Gravitationsfeldes gP an einem Punkt P der Flugbahn durch seine Stärke am Beobachtungspunkt gB ausdrücken: |
|
||||||
|
Somit ergibt sich in den angedeuteten Näherungen der nebenstehende Beschleunigungsvektor durch das Gravitationfeld. Anmerkung: In dem verwendeten Wert für gB geht die radiale Komponente der Zentripetalkraft mit ein. |
|
|
Im Beobachter-Bezugssystem (ENU) ergibt sich für RP: |
|
|
Und in erster Näherung in Re ergibt sich für die Komponenten des Beschleunigungsvektors im Beobachter-Bezugsystem (ENU) : |
|
|
De Komponenten des Beschleunigungsvektors im Flugkörper-Bezugssystem (DCU) sind:
|
|
|
Zum Vergleich: Eine Flugbahn, berechnet mit unterschiedlichen Näherungen für die Gravitationskraft - aber ohne den nichtradialen Zentripetalbeschleunigungsterm. |
|
Die vollständige Variante ... |
Ohne die 1/Re-Korrekturen ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 0,0 | 0,0 | 0,0 ===> größte Höhe: 2406,7 Aufschlagszeit: 44,3384 Aufschlagsort DCU: 8803,8 | 16,0 | 0,0 Aufschlagsort ENU: 84,0 | 8803,8 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU : 0,0 | 0,0 | 0,0 ===> größte Höhe: 2405,9 Aufschlagszeit: 44,3169 Aufschlagsort DCU: 8804,2 | 15,8 | 0,0 Aufschlagsort ENU : 84,2 | 8804,2 | 0,0 |
|
|
Der aerodynamische Luftwiderstand
|
Durch den Luftwiderstand wird ein Flugkörper abgebremst, die Luft muss längs der Flugbahn verdrängt werden. Der Luftwiderstand führt zu einer negativen Beschleunigung in Richtung des Geschwindigkeitsvektors. Im Bereich der Schallgeschwindigkeit von 0,85 Mach bis 1,3 Mach treten zudem mit steigender Geschwindigkeit Stoßwellen auf, die den Luftwiderstand maßgeblich bestimmen. |
|
Die durch den Luftwiderstand verursachte Beschleunigung bR (R steht für Reibung) wird in einem erdgebundenen Koordinatensystem durch die nebenstehende Formel beschrieben:
|
|
|
ρ ist die lokale Luftdichte [kg/m³], sie hängt von der Höhe ab. Kd ist der Luftwiderstandsparameter [m²/kg]. Er hängt von der Form und der Masse des Flugkörpers ab. Ein einfacher Ansatz ist aufgeführt, wobei QFK den Flächenquerschnitt des Körpers bemisst, MFK ist seine Masse. MS ist die Machzahl, gebildet aus Geschwindigkeit des Flugkörpers und der lokalen Schallgeschwindigkeit vS. Cd ist der dimensionslose Luftwiderstandskoeffizient, er hängt von der Geschwindigkeit des Flugkörpers ab, hier über die Machzahl MS eingeführt. Die genaue Form des Koeffizienten variiert mit dem Flugkörper – hier wird ein universelles Modell verwendet. |
|
|
Im Beobachter-Bezugssystem (ENU) ergibt sich: |
|
|
Im Flugkörper-Bezugssystem (DCU) wird das zu: |
|
|
... mit den Komponenten von wFK :
|
|
|
„Im Bereich der Unterschallgeschwindigkeit, d. h. unter 0,85 Mach, ist die einzige atmosphärische Störung eine Turbulenz hinter dem Projektil. Im Bereich der Schallgeschwindigkeit von 0,85 Mach bis 1,3 Mach treten mit steigender Geschwindigkeit Stoßwellen auf. Im unteren Teil dieses Geschwindigkeitsbereichs entstehen Stoßwellen an allen Unebenheiten des glatten Projektilmantels. Wenn die Geschwindigkeit 1 Mach übersteigt, bilden sich vorne und hinten am Projektil Stoßwellen, die sich kegelförmig vom Projektil ausbreiten. Der Winkel an der Spitze ändert sich mit der Geschwindigkeit des Projektils. So ist bei 1 Mach die vordere Stoßwelle im Wesentlichen eine Ebene, bei 1,4 Mach beträgt der Winkel des Kegels ungefähr 90 Grad. Bei 2,48 Mach hat die Stoßwelle, die das Projektil nach sich zieht, an der Spitze einen Winkel von etwas weniger als 50 Grad.“ (Microsoft Encarta 2002) |
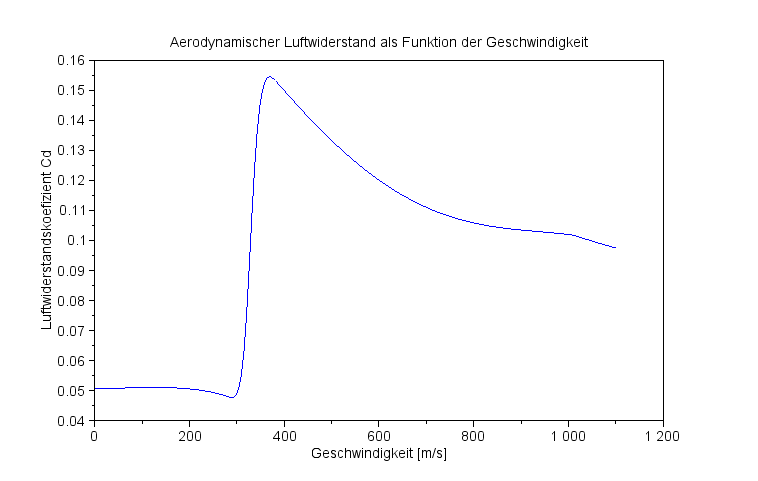
Universelles Modell für den Luftreibungskoeffizienten Cd
|
Der Cd-Koeffizient verdreifacht sich zwar im Umfeld von Mach=1, der Einfluss auf die ballistische Flugbahn hält sich aber in Grenzen – in der folgenden Grafik wird die maximal erreichte Flughöhe bei verschiedenen Anfangsgeschwindigkeiten aufgetragen. |
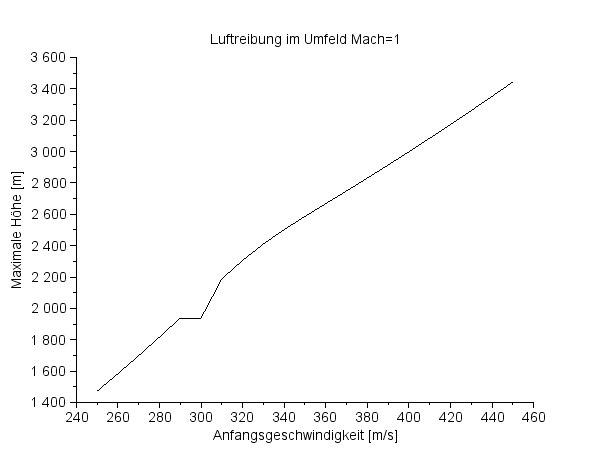
Maximale Höhe gegen Anfangsgeschwindigkeit
|
Zum Vergleich: Eine Flugbahn, berechnet einmal mit und einmal ohne die Berücksichtung der Luftreibung, dann mit Berücksichtung der Luftreibung und unterschiedlichen, in der Höhe konstanten Windgeschwindigkeiten - aber ohne den Zentripetalbeschleunigungsterm. |
|
Mit Luftreibung ... |
Ohne Luftreibung ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 0,0 | 0,0 | 0,0 ===> größte Höhe: 2406,7 Aufschlagszeit: 44,3384 Aufschlagsort DCU: 8803,8 | 16,0 | 0,0 Aufschlagsort ENU: 84,0 | 8803,8 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 0,0 | 0,0 | 0,0 ===> größte Höhe: 2775,7 Aufschlagszeit: 47,6489 Aufschlagsort DCU: 11116,7 | 22,7 | 0,0 Aufschlagsort ENU: 77,3 | 11116,7 | 0,0 |
|
Mit konstantem Wind w=(-10, -10, 0) ... |
Mit konstantem Wind w=(-100, -100, 0) ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: -10,0 | -10,0 | 0,0 ===> größte Höhe: 2370,3 Aufschlagszeit: 43,9955 Aufschlagsort DCU: 8647,4 | 15,5 | 0,0 Aufschlagsort ENU: 84,5 | 8647,4 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: -100,0 | -100,0 | 0,0 ===> größte Höhe: 1919,3 Aufschlagszeit: 39,1737 Aufschlagsort DCU: 6607,4 | 10,4 | 0,0 Aufschlagsort ENU: 89,6 | 6607,4 | 0,0 |
|
Mit konstantem Wind w=(+10, +10, 0) ... |
Mit konstantem Wind w=(+100, +100, 0) ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 10,0 | 10,0 | 0,0 ===> größte Höhe: 2434,1 Aufschlagszeit: 44,594 Aufschlagsort DCU: 8927,0 | 16,3 | 0,0 Aufschlagsort ENU: 83,7 | 8927,0 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 100,0 | 100,0 | 0,0 ===> größte Höhe: 2492,4 Aufschlagszeit: 45,1384 Aufschlagsort DCU: 9277,0 | 17,3 | 0,0 Aufschlagsort ENU: 82,7 | 9277,0 | 0,0 |
|
Mit konstantem Wind w=(-1, -1, 0) ... |
Mit konstantem Wind w=(+1, +1, 0) ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: -1,0 | -1,0 | 0,0 ===> größte Höhe: 2403,5 Aufschlagszeit: 44,3079 Aufschlagsort DCU: 8789,6 | 15,9 | 0,0 Aufschlagsort ENU: 84,1 | 8789,6 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth) : 90 Winddaten ENU: 1,0 | 1,0 | 0,0 ===> größte Höhe: 2409,9 Aufschlagszeit: 44,3679 Aufschlagsort DCU: 8817,6 | 16,0 | 0,0 Aufschlagsort ENU: 84,0 | 8817,6 | 0,0 |
|
|
Der aerodynamische Spineffekt
|
Um die Fluglage zu stabilisieren, können Flugkörper in Eigenrotation um die Längsachse versetzt werden. Diese Rotation verursacht eine Kraft, die den Flugkörper nach rechts aus der Flugbahn-Ebene drückt und so zu einer transversalen Bewegung führt. |
|
Ein einfaches, universelles Modell für diesen Spineffekt ist: bS ist der Beschleunigungsvektor für den Spineffekt. 'S' steht für 'Spin'. λ gibt die Größe des Effektes an. d2 ist der Basisvektor im Flugkörpersystem KFK (DCU), der senkrecht auf der Flugbahn-Ebene steht. ei sind die Basisvektor im Beobachtersystem KB (ENU). |
|
|
Zum Vergleich: Eine Flugbahn, berechnet einmal mit und einmal ohne die Berücksichtung des Spineffektes - aber ohne den Zentripetalbeschleunigungsterm. |
|
Ohne dem Spineffekt ... |
Mit dem Spineffekt ... |
|
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 0,0 | 0,0 | 0,0 ===> größte Höhe: 2406,7 Aufschlagszeit: 44,3384 Aufschlagsort DCU: 8803,8 | 16,0 | 0,0 Aufschlagsort ENU: 84,0 | 8803,8 | 0,0 |
Geodätische Breite: 52 Startschwindigkeit: 330 Richtwinkel: 45 Omega (Azimuth): 90 Winddaten ENU: 0,0 | 0,0 | 0,0 ===> größte Höhe: 2406,7 Aufschlagszeit: 44,3402 Aufschlagsort DCU: 8804,3 | -240,2 | 0,0 Aufschlagsort ENU: 340,2 | 8804,3 | 0,0 |
|
|
||
| © 2014 Bernd Ragutt
Alle Rechte vorbehalten |

|
letzte Änderung: 18.02.2020 Kruschtkiste |
|
|
||
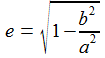
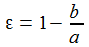
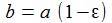
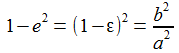
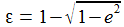
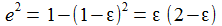
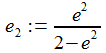
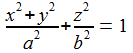
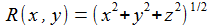
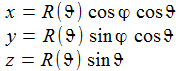
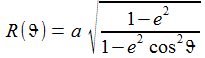
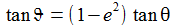
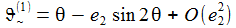
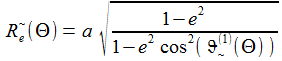
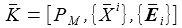
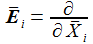
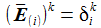
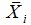 und die sphärischen Polarkoordinaten
und die sphärischen Polarkoordinaten
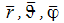 .
.
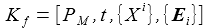
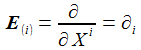
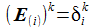
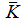 und Kf sind über eine zeitabhängige
Rotation um
die X3-Achse mit dem Winkel ωt wie
folgt verknüpft:
und Kf sind über eine zeitabhängige
Rotation um
die X3-Achse mit dem Winkel ωt wie
folgt verknüpft:
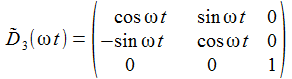
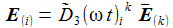
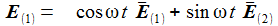
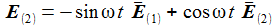
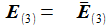
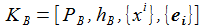
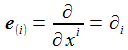
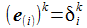
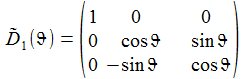
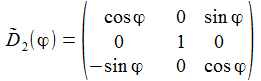
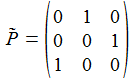
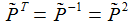
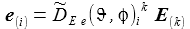
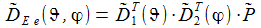
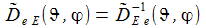
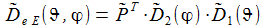
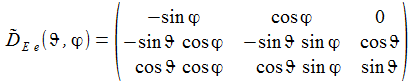
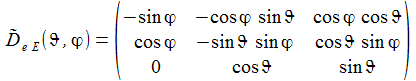
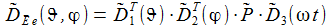
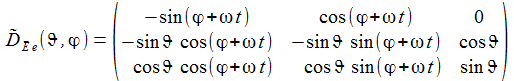
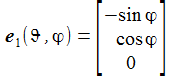
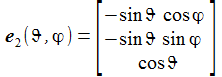
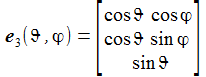
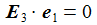
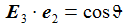
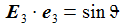
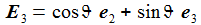
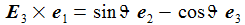
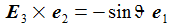
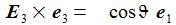
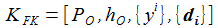
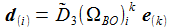
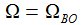
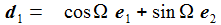
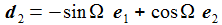
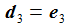
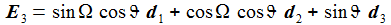
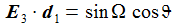
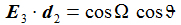
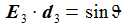
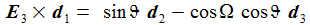
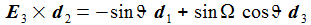
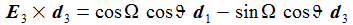
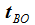 und eine einfache Rotation um die d3-Achse
mit dem Winkel ΘBO verknüpft,
diese Rotation dreht e1
(East) in die Flugbahn-Ebene.
und eine einfache Rotation um die d3-Achse
mit dem Winkel ΘBO verknüpft,
diese Rotation dreht e1
(East) in die Flugbahn-Ebene.
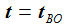
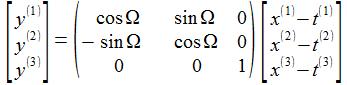
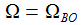

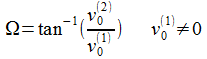

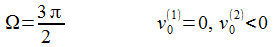
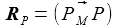
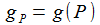
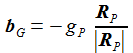
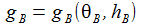
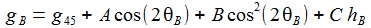
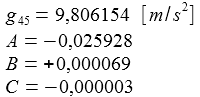
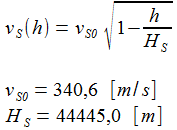
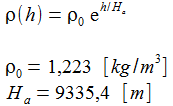
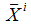 im Inertialsystem
im Inertialsystem
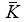 mit denen im
mitbewegten Koordinatensystem
X(i) wie folgt zusammen:
mit denen im
mitbewegten Koordinatensystem
X(i) wie folgt zusammen:
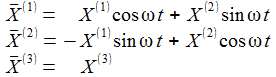
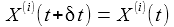
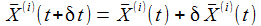
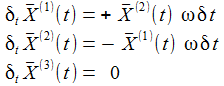

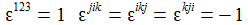
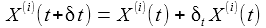
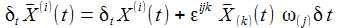
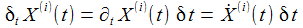
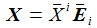
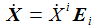
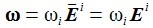
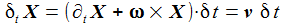
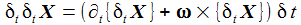
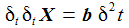
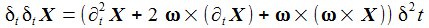
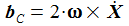
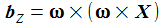
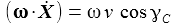
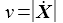
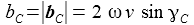
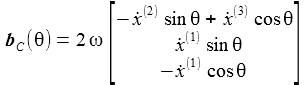
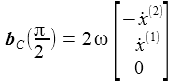
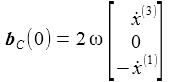
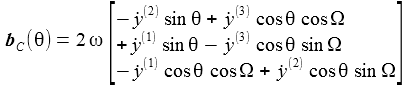
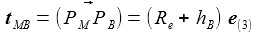
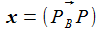
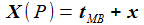
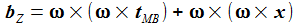
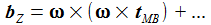
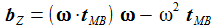
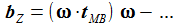
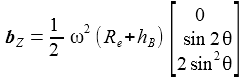
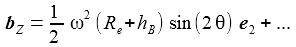
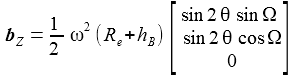
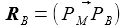
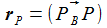
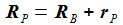
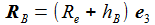
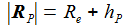
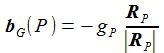
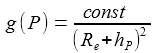
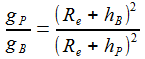
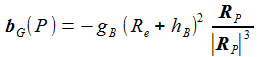
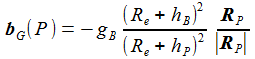
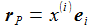
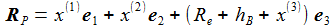
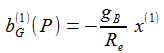
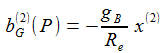
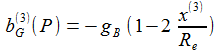
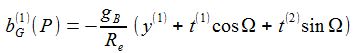
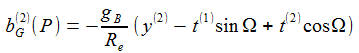
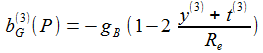
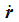 ist
der Geschwindigkeitsvektor relativ zur umgebenden Luft.
Kennt man also aus den Wetterdaten die
Windgeschwindigkeit w in
unterschiedlichen Höhen, so kann man entsprechend auf
den effektiven Geschwindigkeitsvektor
ist
der Geschwindigkeitsvektor relativ zur umgebenden Luft.
Kennt man also aus den Wetterdaten die
Windgeschwindigkeit w in
unterschiedlichen Höhen, so kann man entsprechend auf
den effektiven Geschwindigkeitsvektor
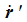 korrigieren.
korrigieren.