Das Doppelpendel

Ein nicht-lineares Problem
»Zwei starre gekoppelte Pendel«

Numerisch gelöst und animiert
mit dem
»Werkzeugkasten SciLab«

Prolog

Als ich in den siebziger Jahren des letzten Jahrtausends Physik studierte, stanzte ich Fortran-Code in Lochkarten – unvergessen ist mir ein 'berechnetes GOTO' in einer Übungsaufgabe. Als Ergebnis erhielt man am nächsten Tag aber nur einen Haufen Zahlen. Die Veranschaulichung von physikalischen Vorgängen war (fast) nur im Experiment möglich.

Anfang der achtziger Jahren hatte dann jeder Physiker einen Commodore C64. Ich wollte mir den Schmetterlingseffekt veranschaulichen, der bei nicht-linearen Differentialgleichungen auftritt: Eine nur kleine Änderung bei den Anfangsbedingungen kann dabei zu einem ganz anderen Lösungsverhalten führen.

Ich programmierte zunächst in Assembler und Forth, in Pascal setzte ich dann das Runge-Kutta-Verfahren zur Lösung von Differentialgleichungen um und spendierte dem Ganzen - dank dem Kleinod C64 - eine graphische Ausgabe. Ich haderte jedoch mit dem Speicherplatz (64K).

Ein extra für 200 DM gekaufter Compiler von Data-Becker sollte Abhilfe schaffen und eine 'Segmentierung' erlauben, aber genau diese Compiler-Eigenschaft war nur ein Werbeversprechen und funktionierte nicht.

Dem C64 folgte (leider) bald ein Atari, ein an sich vorzüglicher Rechner im Macintosh-Stil, das Software-Angebot war aber insgesamt ärmlich und meist von dürftiger Qualität, der PC war bereits der große Konkurrent. Für die Textverarbeitung benutzte ich das famose 'Signum', für andere Dinge gab es auf dem schwarzen Markt einen Macintosh-Emulator. Ein Compiler war nicht im Angebot.

Heute dagegen gibt es großartige Werkzeuge, die noch nicht einmal etwas kosten, etwa »LibreOffice«, mit dem ich diese Zeilen und die mathematischen Formeln schreibe oder aber den MatLab-Nachbau »SciLab«.

Ich habe mir das starre Doppelpendel ausgesucht, um ein kleines physikalischen Problem zu lösen und zu veranschaulichen.

Das Problem

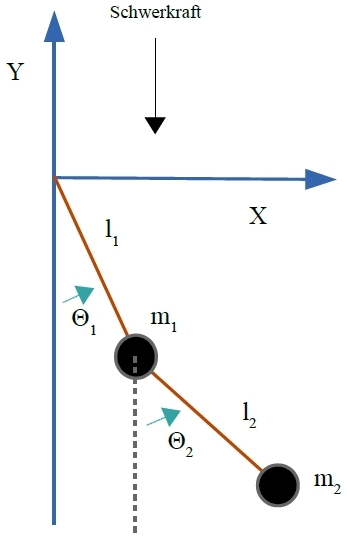
Zwei Ku­geln mit den Massen m1 und m2 sowie zwei Stan­gen der Län­gen l1 und l2 sol­len ein schwin­gen­des Sys­tem bil­den, das zwei Frei­heits­gra­de hat.

Es soll hier nur die Schwer­kraft wirken, die Coriolis­kraft, die durch die Erd­ro­ta­tion her­vor­geru­fen wird, und die Rei­bungs­kräf­te, die et­wa durch die Luft ent­ste­hen, wer­den ver­nach­läs­sigt.

Das Prob­lem wird als ebe­nes Prob­lem be­han­delt – ob­wohl es durch­aus span­nend wä­re, die Be­we­gung­sviel­falt in drei Di­men­sio­nen zu be­trach­ten.

Die physikalische Algorithmik

Die New­ton­schen Be­we­gungs­glei­chun­gen in einem zwei­dimen­siona­len karte­sischen Koor­dina­ten­system (x,y) las­sen sich schnell auf­stel­len, denn es wirkt auf die Mas­sen m1 und m2 allein die kon­stante Schwer­kraft der Stärke g in die nega­tive y-Rich­tung. Das Pen­del schwingt daher in einer fixen Ebene.

Die beiden Massen werden als Punkt­massen behan­delt und die beiden Ver­bin­dungs­stangen als starr und masse­los.


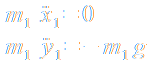
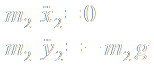
Die kar­te­sis­chen Ko­or­di­na­ten der Punkt­massen er­fül­len mit der Kon­stanz der Län­gen der Ver­bin­dungs­stangen zwei Zwangs­be­din­gun­gen, das Pro­blem hat da­her nur zwei Frei­heits­grade:

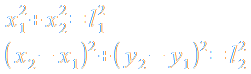
Als ge­ne­ra­li­sier­te Ko­or­di­na­ten zur Beschreibung der beiden Freiheitsgrade wer­den die Aus­lenk­win­kel Θ1 und Θ2 ver­wen­det:


   

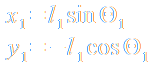
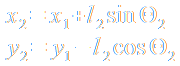
Die ki­ne­ti­sche Ener­gie T er­gibt ich wie folgt aus den Ge­schwin­dig­kei­ten:

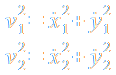
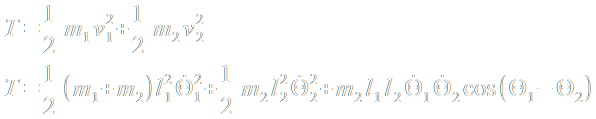
Die po­ten­tiel­le Ener­gie V ist:

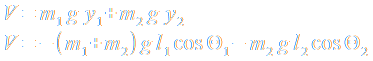
Ich lei­te die Be­we­gungs­glei­chun­gen mit­hilfe des La­gran­ge-For­ma­lis­mus ab. Die bei­den Be­we­gungs­glei­chun­gen er­ge­ben sich aus der La­gran­ge-Fun­ktion und den La­gran­ge­schen Glei­chun­gen:

Die La­gran­ge-Fun­kti­on L ist ein­fach die Diffe­renz aus kine­tischer und poten­tieler Energie:

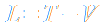
Aus der La­gran­ge-Funk­ti­on er­hält man die Be­we­gungs­glei­chun­gen durch flei­ßi­ges Ab­lei­ten mithilfe der La­gran­ge­schen Glei­chun­gen:

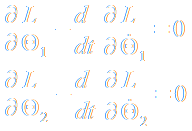
Und hier sind sie in voller Schön­heit, die bei­den Be­we­gungs­glei­chun­gen:

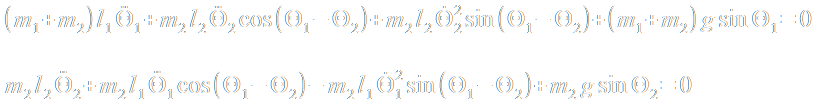
Die mathe­ma­ti­sche Nu­me­rik

Um die Lö­sungs­ma­schi­ne Sci­Lab ein­set­zen zu kön­nen, wer­den in ei­nem ers­ten Schritt die bei­den Dif­fe­ren­tial­glei­chnu­gen zwei­ter Ord­nung in vier Dif­fe­ren­tial­glei­chun­gen ers­ter Ord­nung um­ge­wan­delt.

Da­zu wer­den zwei neue Va­ri­ab­len ein­ge­führt, der Schritt wird hier aber nicht vor­ge­führt:

Das Um­set­zen der ma­the­ma­ti­schen Glei­chungen in Sci­Lab-Co­de ist hand­werk­li­che Klein­ar­beit.

Die Dateien des Sci­Lab-Co­des ha­be ich in ein Ver­zeich­nis ge­steckt und zu einer zip-Da­tei ge­packt. Den Scilab-Code mit etwas Mathematik habe ich zudem in einer PDF-Datei zusammen­gefasst. Sie kön­nen sich diese hier bei Interesse her­un­ter­la­den:

Im Sci­lab-Co­de wer­den erst al­le Punk­te be­rech­net, 10 bis 15 Punk­te in der Se­kun­de - dann wird ge­zeich­net.

Die Aus­ga­ben in das Gra­fik-Fens­ter von Sci­Lab ha­be ich mit dem net­ten Werk­zeug Cam­Studio zu avi-­Vi­de­os mit­ge­schnit­ten. Der 'Mi­ro Vi­deo Con­ver­ter' er­zeugt aus den avi-­Da­teien Film­chen im kom­pak­teren WebM-For­mat.

Der Sci­Lab-­Code tut in et­wa, was er soll, er wird aber kei­nen Schön­heits­preis er­hal­ten. Die An­fangs­be­din­gun­gen sind in blau­er Schrift her­vor­ge­ho­ben.

Ein Hin­weis: Un­ter den De­mos, die mit dem Werk­zeug­kasten Sci­lab ein­her­kommen, gibt es auch ein sehr hüb­sches 10-fach-Pen­del zu be­stau­nen. Al­ler­dings ist hier zum Erstel­len des Quell­codes ein wei­te­res Werk­zeug, Maple, vor­ge­schal­tet worden und es wird For­tran-Code er­zeugt, der erst noch kom­pi­liert werden muss; der Fortran-Com­piler dazu muss als zusätz­liches Werk­zeug instal­liert werden.

Die Bei­spiel-Vi­deos

Nur 10 bis 15 Bilder sind es pro Sekunde in den Videos - mein kleiner Rechner war zu lahm für den SciLab-Code, der ja interpretiert wird.

Die Filmchen liegen im WebM-Format mit je­weils unterschiedlichen Anfangsbedin­gun­gen vor.

Bit­te be­nut­zen Sie die einge­blen­deten Steuer­elemente, gege­benen­falls auch die rech­te Maus­tas­te und das Kon­text­me­nü, um die Fil­me zu star­ten.

Mein Doppelpendel schwingt mit den nach­fol­gend auf­ge­führ­ten Längen und Massen; die anfänglichen Aus­lenk­ungs­win­kel Φi(0) und Winkelge­schwin­dig­keiten dΦi(0)/dt=ωi(0) der Massen sind ober­halb der Videos auf­geführt; bei eini­gen Videos habe ich auch die Mas­sen vari­iert, die stehen dann unter­halb der Videos.

l1 = 1,0 m

l2 = 0,5 m

m1 = 1,0 kg

m2 = 0,5 kg

Ein kleiner pendel­tech­nischer Hinweis:
Die Pen­delmassen sollen hier Voll­kreise aus­füh­ren kön­nen.

|  Θ1(0) = 30°  |  Θ2(0) = 30°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

Nur ein leichtes Schwingen
- hin und her -
fast wie ein Pendel ...

|  Θ1(0) = 0°  |  Θ2(0) = 0°  |  ω1(0) = 0 rad/s  |  ω2(0) = 1 rad/s  |

Ein stehender Propeller ...
- quasi am Stock
sich drehend

|  Θ1(0) = 50°  |  Θ2(0) = -50°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

Es zappelt arg hin und her
- und macht dann doch so
eben einen Über­schlag

|  Θ1(0) = 50°  |  Θ2(0) = -50°  |  ω1(0) = 1 rad/s  |  ω2(0) = 1 rad/s  |

Ein elegantes Schwin­gen
- sehr harmo­nisch -
mit Übers­chlägen

|  Θ1(0) = 50°  |  Θ2(0) = -50°  |  ω1(0) = 1 rad/s  |  ω2(0) = 1,5 rad/s  |

Ein überstürzter Start
- dann mehr tän­zelnd -
mit schönen Saltos

|  Θ1(0) = 50°  |  Θ2(0) = -50°  |  ω1(0) = 10 rad/s  |  ω2(0) = 9,5 rad/s  |

Ein großes Kreisen
mit heftigen Innen­saltos
und gelas­senem Schwingen

|  Θ1(0) = 0°  |  Θ2(0) = 0°  |  ω1(0) = -4 rad/s  |  ω2(0) = 4 rad/s  |

Bei aller Mühe
- es bleibt doch nicht
beim Innen­kreiseln

|  Θ1(0) = 0°  |  Θ2(0) = 0°  |  ω1(0) = 5 rad/s  |  ω2(0) = 6,25 rad/s  |

Ein schönes Innen­rollen
- Schafft er es oder nicht,
den großen Über­schlag?

|  Θ1(0) = 0°  |  Θ2(0) = 0°  |  ω1(0) = 20 rad/s  |  ω2(0) = 24,7 rad/s  |

Das große Kreisen,
der Kleine folgt,
ob er will oder nicht

|  Θ1(0) = 0°  |  Θ2(0) = 0°  |  ω1(0) = 20 rad/s  |  ω2(0) = 22,5 rad/s  |

Das große Kreisen,
der Kleine pro­pel­lert,
der Große kreist

|  Θ1(0) = 80°  |  Θ2(0) = 80°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

Die untere Kugel ist nun
ein Stück­chen leichter
m1 = 5 kg  |  m2 = 0,5 kg

|  Θ1(0) = 80°  |  Θ2(0) = 80°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

Die obere Kugel ist
nun die leichtere
m1 = 0,5 kg  |  m2 = 5 kg

|  Θ1(0) = 179°  |  Θ2(0) = 181°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

m1 = 5 kg  |  m2 = 5 kg
Beide Kugeln beginnen den
Fall von fast ganz oben

|  Θ1(0) = 181°  |  Θ2(0) = 180°  |  ω1(0) = 0 rad/s  |  ω2(0) = 0 rad/s  |

m1 = 5 kg  |  m2 = 5 kg
Die eine Kugel ist ganz oben
die andere fast ganz oben