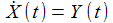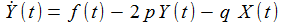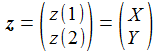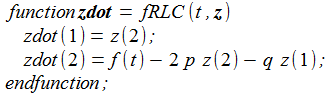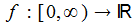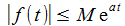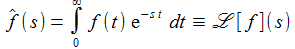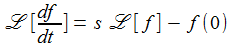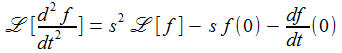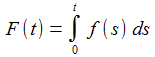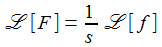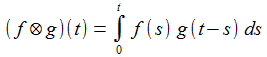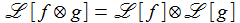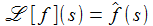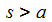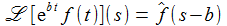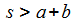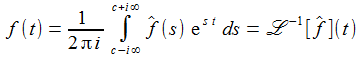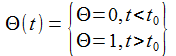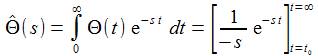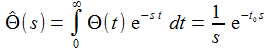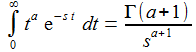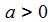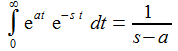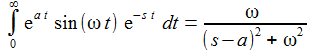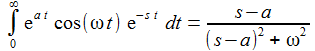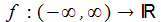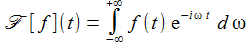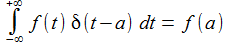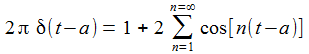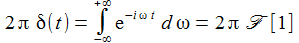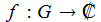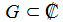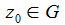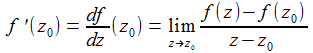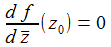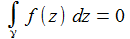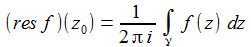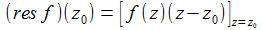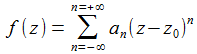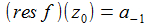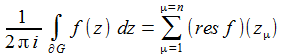|
|
Einfache Schwingkreise mit SciLab |
|
|
|
|
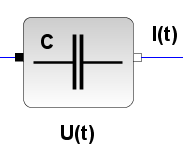
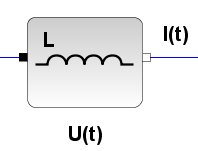
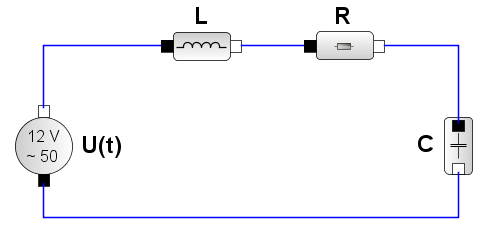
Bauteile
|
|
|
|
|
|
|
|
|
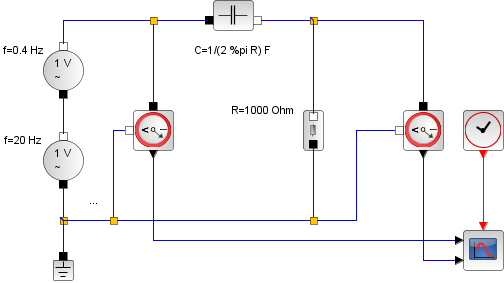
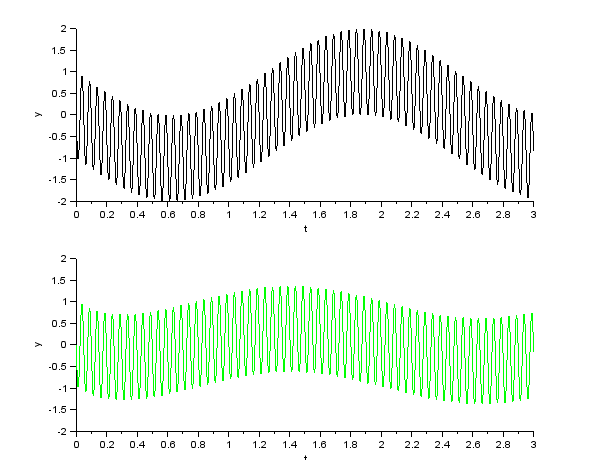
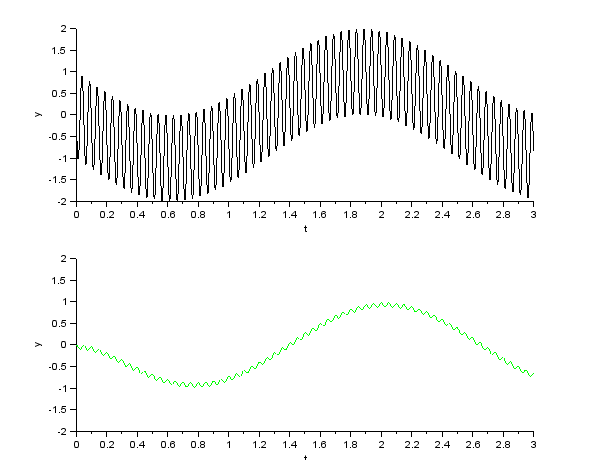
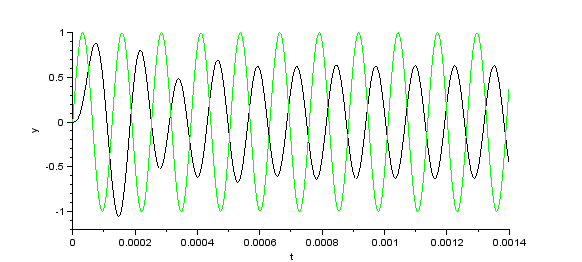
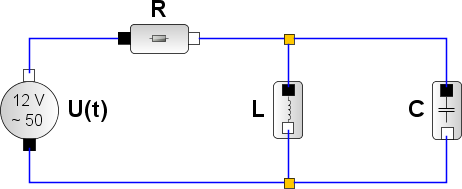
Anstatt gleich schweres Geschütz aufzufahren, sollte man natürlich mit einfachen Fragen beginnen: „Wie verhalten sich die Bauteile einzeln in einem Gleichstrom-Stromkreis?“, „Wie verhalten sich die Bauteile in einem Wechselstrom-Stromkreis?“ Kein Problem, mit dem Baukasten Xcos lassen sich in SciLab symbolische Blöcke zu Schaltkreisen zusammenstellen, die sich ausführen lassen. Hier zwei Beispiele, die sich auf den gleichen Schaltkreis beziehen: Ein einfaches RC-Glied wird jeweils mit zwei Wechselspannungen unterschiedlicher Frequenzen (0,4 und 20 Hertz) gespeist. Zunächst wird die Spannung am Widerstand UR und die Eingangsspannung Ui gemessen uud ausgegeben, dann wird die Spannung am Kondensator UC und die Eingangsspannung gemessen aud ausgegeben. Die Eingangsspannung ist schwarz gezeichnet, die Ausgangsspannung grün. |
|
Ein Hochpassfilter mit Xcos |
|
Das Hochpass-Filter filtert tiefe Frequenzen! |
|
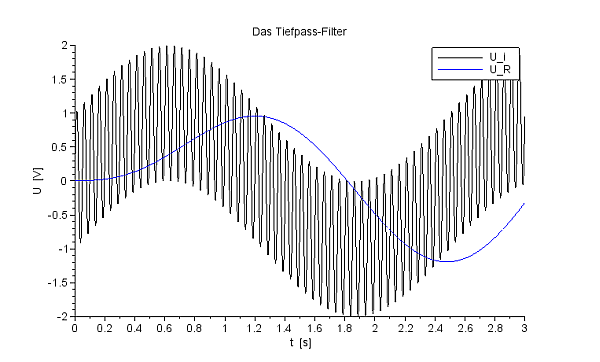
Ein Tiefpass-Filter mit Xcos |
|
Das Tiefpass-Filter filtert hohe Frquenzen |
|
Einfach und eindrucksvoll. Das Hochpass-Filter lässt also hohe Frequenzen passieren, das Tiefpass-Filter eben tiefe. Da für die Spannungen Ui=UR+UC gilt, ergäbe sich natürlich aus der einen Lösung gleich auch die andere. |
|
|
Der Serienschwingkreis
Differentialgleichungen
|
|
|
Die Kirchhoffschen Gesetze für elektrische Stromkreise verbinden die Ströme durch und die Spannungen an den Bauteilen des einfachen Schaltkreises. Die zeitabhängige Eingangsspannung ist Ui. |
|
|
Bei gegebener Eingangsspannung Ui(t) erhält man die Differentialgleichung für den Strom im Schwingkreis: |
|
|
Die allgemeine Lösung I(t) dieser DGL setzt sich zusammen aus einer partikulären Lösung der inhomogenen DGL und zwei linear unabhängigen Lösungen der zugeordneten homogenen DGL zusammen. Die Größe 'df' steht für die Dämpfungskonstante, der Index 's' steht für 'Schwingungsfaktor'. |
|
|
Die homogenen Lösungen verschwinden allerdings mit wachsendem t, sodass die stationäre Lösung durch die partikuläre Lösung bestimmt wird. |
|
Sinusförmige Eingangsspannung
Lösungssuche
|
Der Schwingkreis soll nun von außen durch ein sinusförmiges Anregungssignal stimuliert werden. Gesucht wird eine partikuläre Lösung, wobei man am besten in der komplexen Ebene rechnet. |
|
|
Die Kreisfrequenz der Eingangsspannung ist ω. Meine Eingangsspannung ist der Imaginärteil. Der Index '0' steht für 'Maximalwert'. |
|
|
Der Schaltkreis wird mit der Anregungsfrequenz ω oszillieren, ich mache daher den einfachen Ansatz mit den beiden noch zu bestimmenden reellen Konstanten I0 und δ. |
|
|
Setzt man den Ansatz in die DGL für I(t) ein, erhält man eine zeitunabhängige Beziehung, aus der sich die beiden Unbekannten aus Betrag und Phase berechnen lassen. |
|
|
|
|
|
|
|
|
ω ist die Anregungskreisfrequenz und ωr die Resonanzkreisfrequenz: |
|
|
Damit erhält man den asymptotischen oder stationären Stromanteil im seriellen Schwingkreis und weiter die Spannung am Widerstand, die am Kondensator und die an der Spule. Der Pfeil bedeutet: 'Strebt asymptotisch gegen'. |
|
|
Und die Gesamtspannung an Kondensator und Spule ist: |
|
|
Ist die Anregungsfrequenz gleich der Resonanzfrequenz, so schließt sich das LC-Glied sozusagen kurz: Die Gesamtspannung an Spule und Kondensator ist nun identisch null und der Strom und die Spannung am Widerstand sind phasengleich. |
|
|
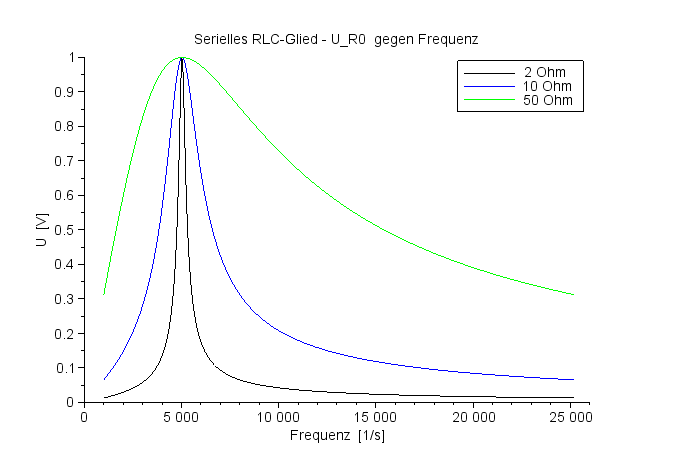
Das Diagramm zeigt den Amplitudengang der Spannung am Widerstand gegen die Anregungsfrequenz ω für drei verschiedene Widerstandswerte. |
|
||||
|
Amplitudengänge der Spannung am Widerstand |
|||||
|
Für kleine Widerstände zeigt der Verlauf eine scharfe Spitze bei der Resonanzfrequenz 5033 Hertz. Die Frequenzen außerhalb eines Bandes um die Resonanzfrequenz werden mehr oder weniger stark unterdrückt. |
|||||
|
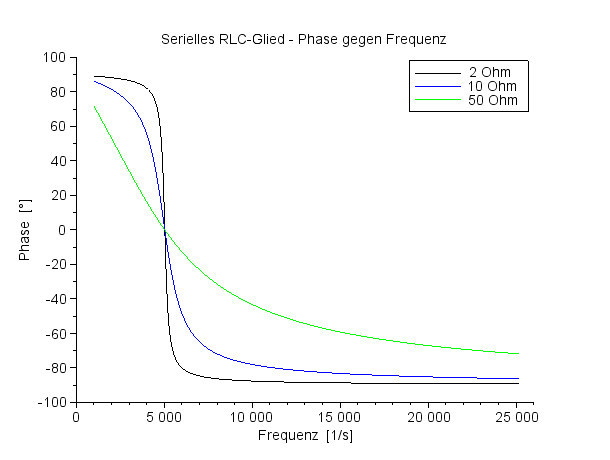
Der Phasenverlauf zwischen dem Strom und der Spannung am Widerstand wird ebenfalls stark durch den Widerstandswert geprägt, je kleiner der Widerstand ist, um so steiler ist der Phasensprung bei der Resonanzfrequenz 5033 Hertz des Serienschwingkreises. |
|
||||
|
Phasenverläufe zwischen Strom und Spannung am Widerstand |
|||||
|
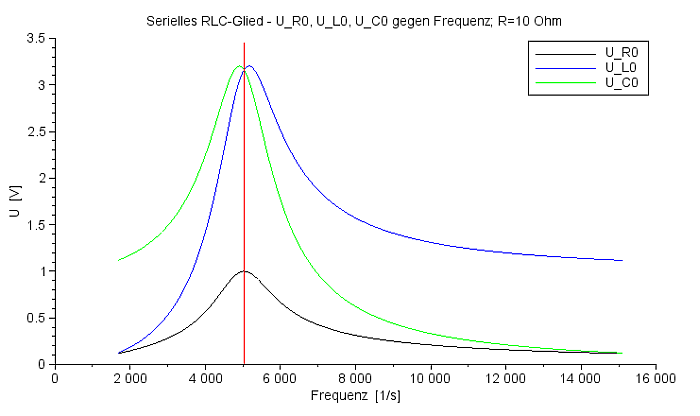
Die Amplituden der Einzelspannungen am Kondensator und an der Spule zeigen das Phänomen der Resonanzüberhöhung in der Nähe der Resonanzfrequenz. |
|
||||
|
Amplitudenverläufe der drei Spannungen bei R=10 Ohm |
|||||
|
Die Einzelamplituden der Spannungen an Spule und Kondensator können ein Vielfaches der Amplitude der Eingangsspannung betragen. Man beachte aber, dass die Summe der beiden Einzelspannungen im Resonanzfall verschwindet, denn die Spannungen an Spule und Kondensator sind im Resonanzfall um 180° phasenverschoben. Die Maxima der drei Amplituden sind wegen der Dämpfung durch den Widerstand leicht verschoben, nur die Spannung am Widerstand ist bei der Resonanzfrequenz maximal. Nicola Tesla hat die Spannungsüberhöhung in seinem Tesla-Transformator ausgenutzt, um die Spannungen hochfrequenter Ströme auf mehrere Millionen Volt zu steigern. |
|||||
|
Eine kleine 'Kurvendiskussion' führt zu den entsprechenden Resonanzfrequenzen für die Spannungsverläufe am Spule und Kondensator. |
|
||||
Das vollständige Zeitverhalten
|
Meist werden nur die stationären Lösungen der Schwingkreise vorgestellt – ich möchte mir einfach so die zeitlich vollständige Lösung für die Spannungen anschauen. Die Differentialgleichungen müssen dazu auf den Tisch. Ua steht für die gerade angepeilte Spannung. |
|
|
|
|
|
Spannung am Kondensator |
|
|
|
|
|
Spannung an der Spule |
|
|
|
|
|
Spannung am Widerstand |
|
|
|
|
|
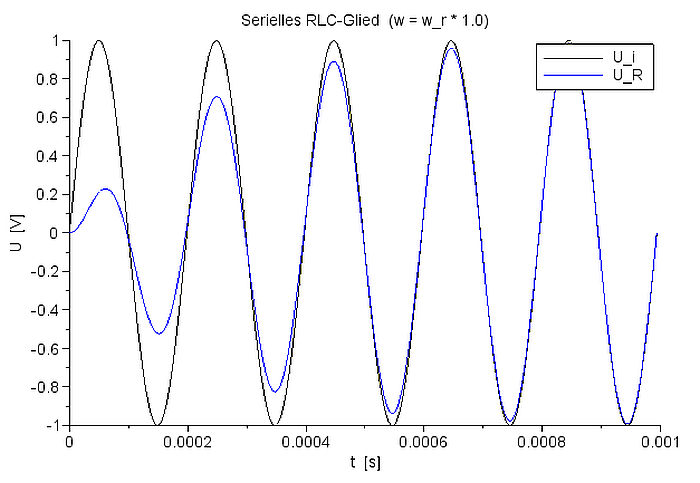
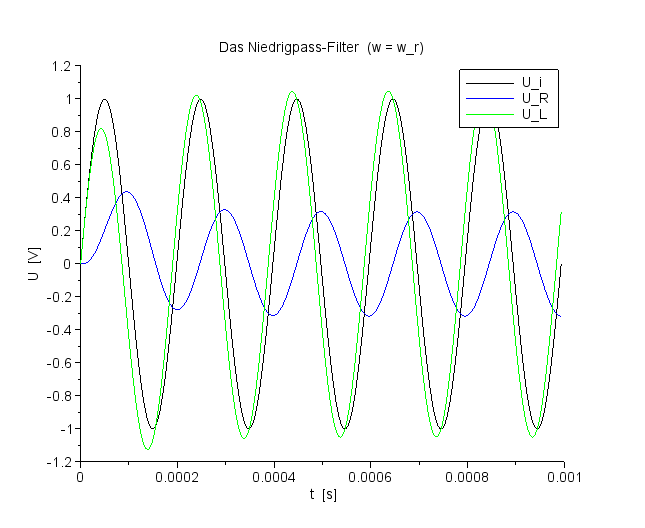
Die drei DGLn unterscheiden sich also nur in der Inhomogenität, der Eingangsgröße. Für drei verschiedene Anregungsfrequenzen soll nun der zeitlich Spannungsverlauf berechnet werden. Die sinusförmige Eingangsspannung ist als schwarze Kurve zu sehen. Als Anregungsfrequenzen werden gewählt: ωr - 1½ ωr - ½ ωr . |
|
|
Die Anfangsbedingungen sind immer dieser Art: |
|
|
Ui(t) = Ui0 sin(ω t)
Die Resonanzfrequenz für den Schaltkreis ist Ua(t): |
R=10; // Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz Ui0=1; // Volt |
|
Zeitlicher Spannungsverlauf für UR bei f=ResFreq |
|
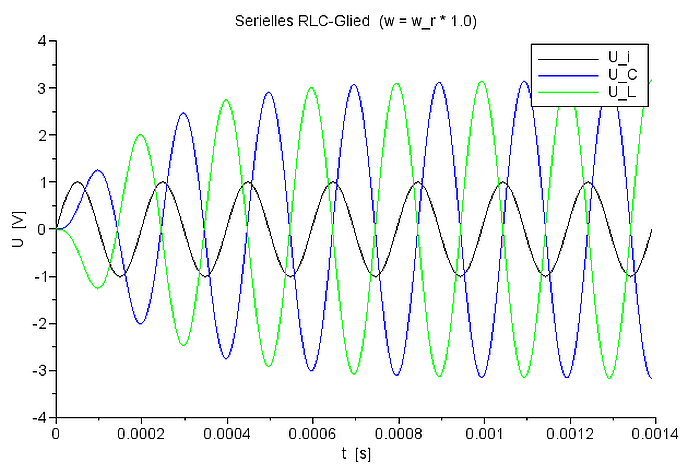
Spannungsverlauf für UC und UL bei f=ResFreq |
|
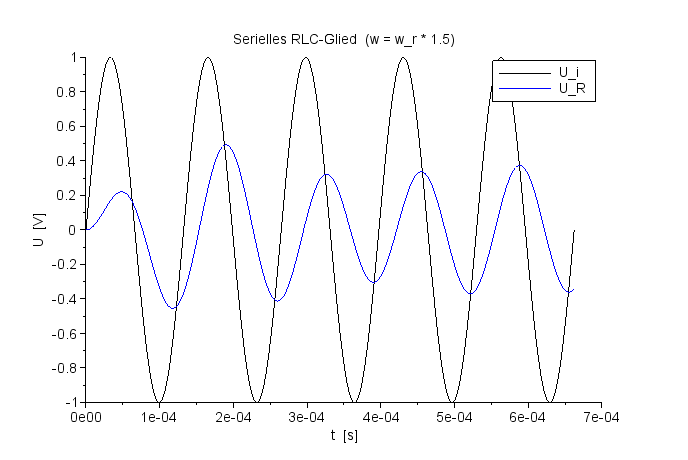
Spannungsverlauf für UR bei f=ResFreq*1,50 |
|
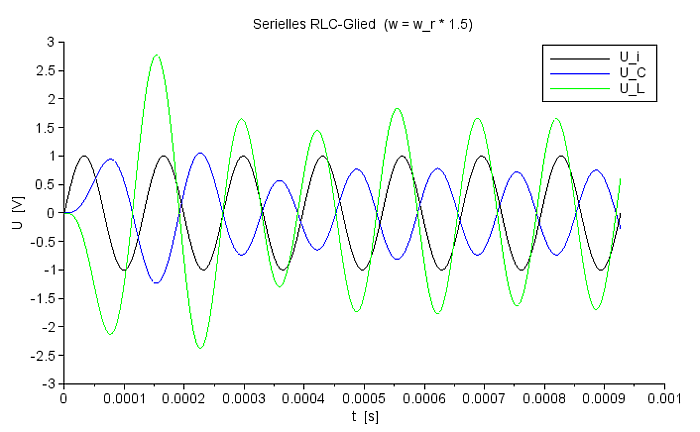
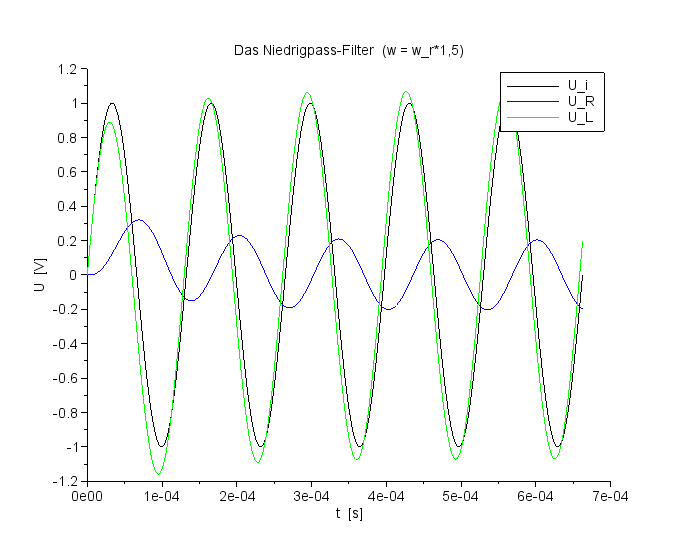
Spannungsverlauf für UC und UL bei f=ResFreq*1,50 |
|
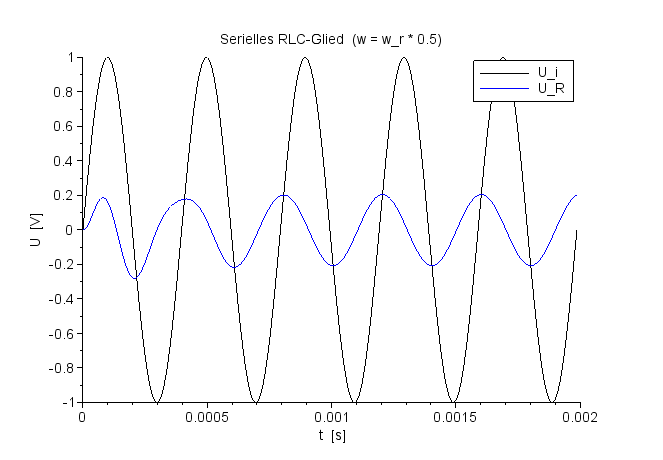
Spannungsverlauf für UR bei f=ResFreq*0,50 |
|
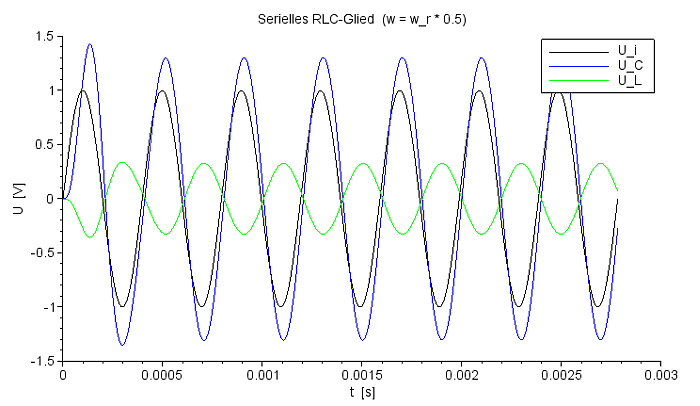
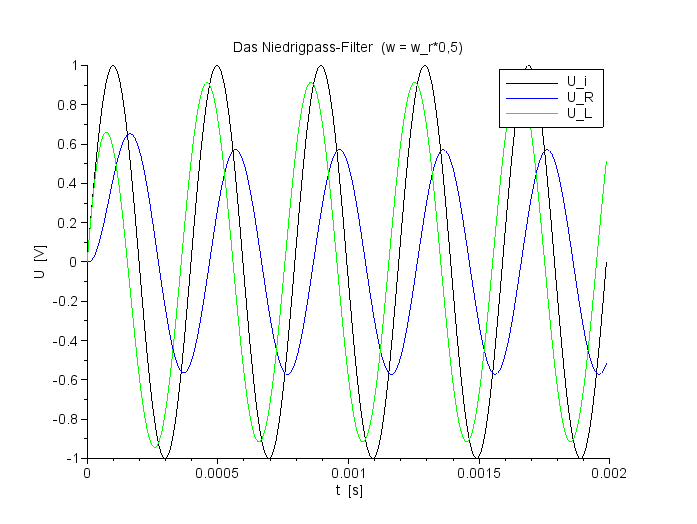
Spannungsverlauf für UC und UL bei f=ResFreq*0,50 |
Zweifachfrequenzantrieb
|
Ui(t) = Ui0 sin(2π f1 t) + Ui0 sin(2π f2 t) Die Resonanzfrequenz für den Schaltkreis ist 0,4 Hertz. Ua(t): |
R=10,0; // Ohm L=3,165; // Henry C=0,05; // Farad ResFreq=0,4; // Hertz Ui0=1; // Volt f1=20,0; // Hertz f2=0,4; // Hertz |
|
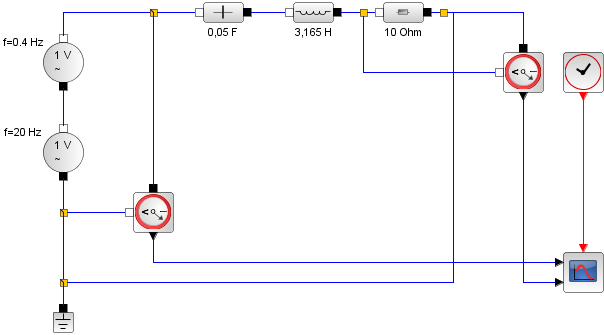
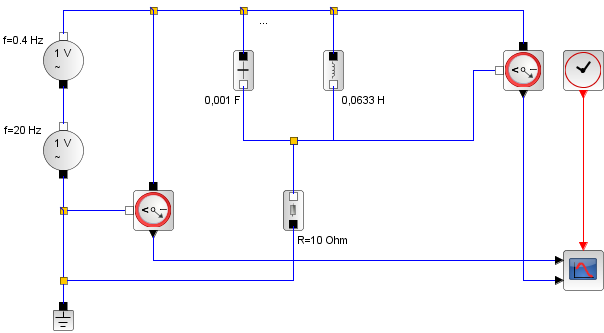
Xcos-Blockschaltbild |
|
|
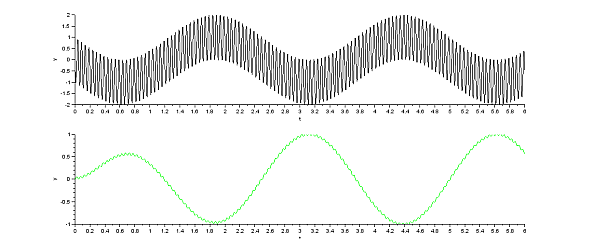
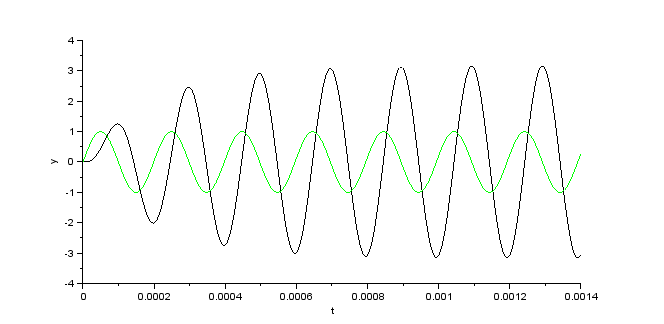
Spannungsverlauf für Ui und UR (grün) |
|
Lineare zeitlich-kontinuierliche Systeme im Zustandsraum
|
Ein System S werde durch einen Zustandsvektor x beschrieben. Angetrieben durch einen Vektor von Eingangsgrößen ui verändert sich das System zeitlich in linearer Weise. |
|
|
Die Änderung des Zustandsvektors wird durch 2 Matrizen A und B beschrieben, die Matrix A ist quadratisch. |
|
|
Ein Beobachter misst einen Satz von Ausgangsgrößen yB, die Ausgangsgrößen sollen in einem linearen Zusammenhang mit dem Systemzustand und den Eingangsgrößen stehen. |
|
|
Solche System lassen sich mit dem SciLab Xcos-Block CLSS (Continuous State-Space System) erfassen. |
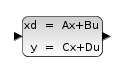
|
|
Über eine Variation der Konstanten lässt sich auch eine geschlossene Lösung angeben: Die SciLab-Funktion 'csim' kann hier zur Berechnung einspringen. |
|
|
Der serielle Schaltkreis-Widerstand, Spule und Kondensator in Reihenschaltung - soll nun als ein lineares System in einem geeigneten Zustandsraum beschrieben werden. Als Zuvstandsvariablen werden der Strom I und die Spannung am Kondensator UC gewählt. |
|
|
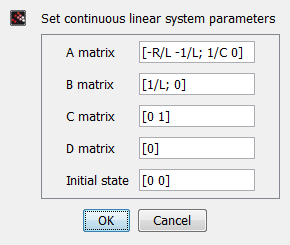
Die beiden Gleichungen zur Beschreibung des Systems sind: |
|
|
Bringt man die Ableitungen auf die linke Seite, lässt sich die Matrizengleichung ablesen: |
|
|
Die Systemgleichung beschreibt die Änderungen im System unter dem Einfluss der einen Eingabegröße Ui. |
|
|
Die eine Messgröße Ua ist die Spannung am Kondensator, daher ist die Beobachtergleichung: |
|
Sinusförmige Eingangsspannung
Eine Lösung mit Xcos
|
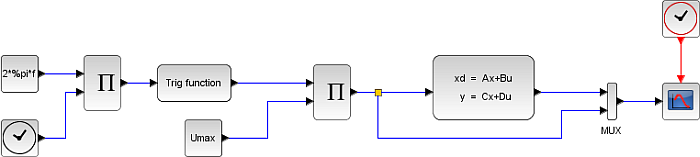
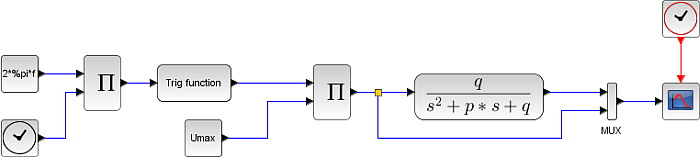
Dieses Gleichungssystem soll nun mit den symbolischen Hilfsmitteln von SciLab, Xcos genannt, gelöst werden. Das Matrizensystem nimmt der zentrale Bock 'Continuous state-space system' (CLSS) auf, der ganze linke Teil des Diagramms erzeugt nur die Eingangswechselspannung der Frequenz f, der rechte Teil dient der Ausgabe. Mein erstes funktionierendes Xcos-Blockschaltbild! |
|
Xcos-Block-Diagramm für das 'Continuous state-space system' |
|
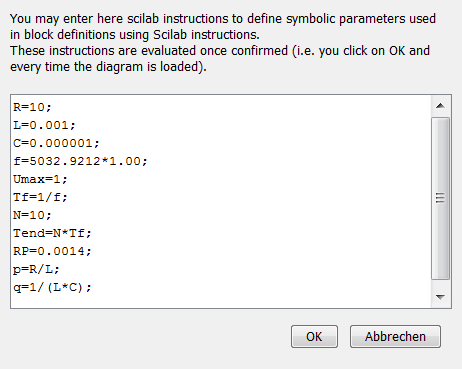
Die Kontext-Parameter |
Die Matrizen |
|
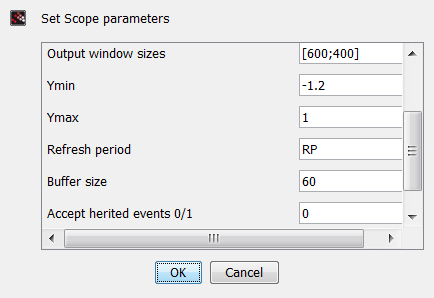
An verschiedenen Stellen müssen verschiedene Zeiten für die Simulation gesetzt werden. Das Zusammenwirken der Zeiten erschließt sich für den Anfänger auch aus der Dokumentation nicht ohne Weiteres. Es brauchte bei mir einige Probiererei. |
|
|
Block CSCOPE: 'Refresh period' |
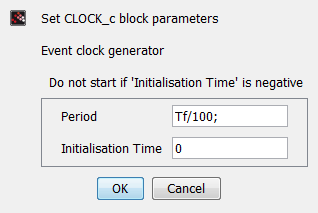
Block CLOCK_c: 'Period' |
|
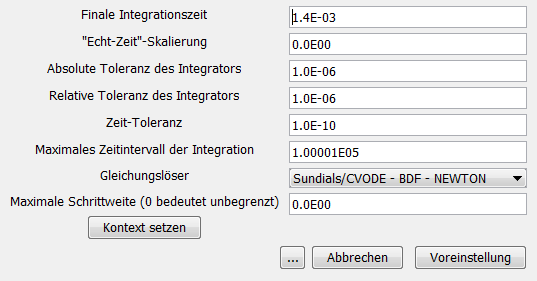
Dialog 'Simulation -> Einstellungen': 'Finale Integrationszeit' |
|
|
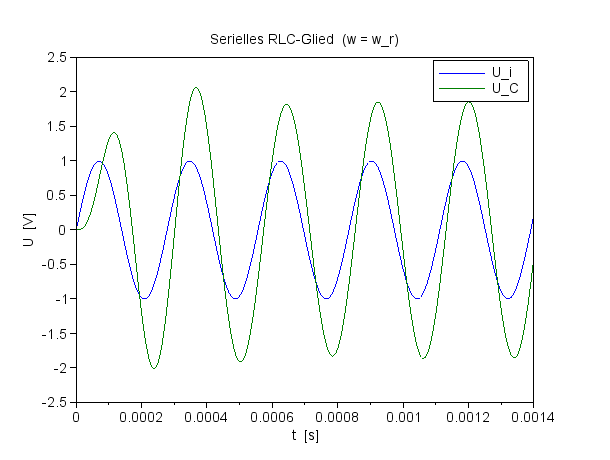
Voilà! Der Spannungsverlauf für die Spannung am Kondensator mit einer Anregungsfrequenz von ωr. |
|
|
Spannungsverlauf für UC (schwarz) bei f=ResFreq |
|
Eine Lösung mit 'csim'
|
Diese hübschen Blockschaltbilder, die man auch ausführen kann, haben mich fasziniert – aber ein leichteres und schnelleres Spiel hatte ich damit nicht, im Augenblick bevorzuge ich doch noch einige Zeilen Quellcode:
|
|
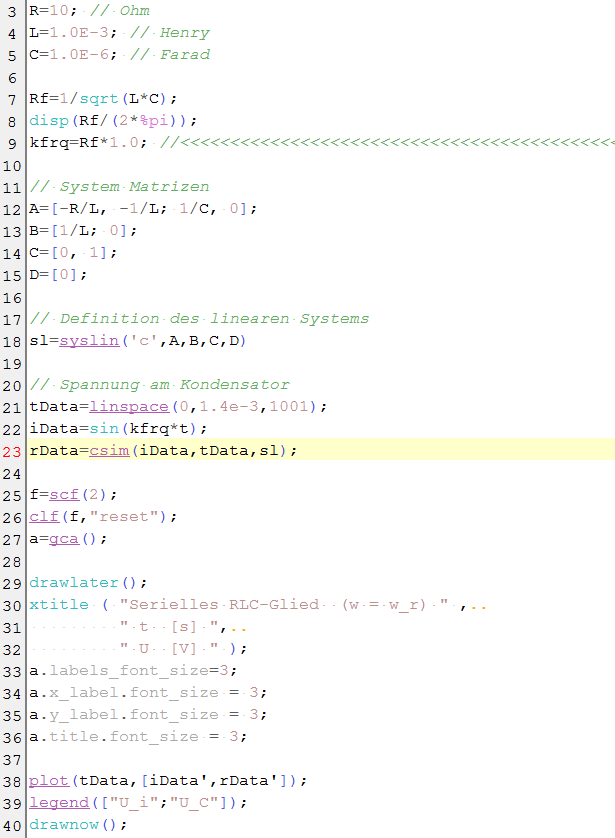
Quellcode für UC mit 'csim' |
|
Viele
Wege führen nach Rom |
Einschaltvorgang bei konstanter Spannung
|
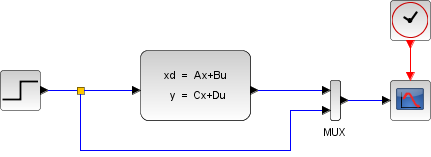
Statt einer Wechselspannung soll nun eine Gleichspannung von 1 Volt angelegt werden, die zur Zeit t=0 eingeschaltet wird. Mit einem Blockdiagramm ist das schnell getan, es wird eine Stufenfunktion verwendet: |
Xcos-Blockschaltbild |
|
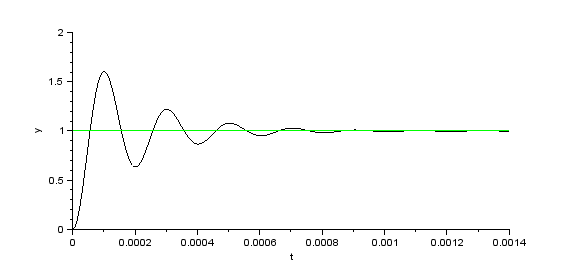
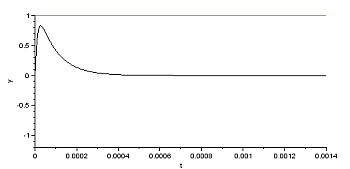
Wohlbekannt, das ist Einschwingvorgang beim Einschalten einer Gleichstromquelle – er ist beendet, wenn der Kondensator aufgeladen ist, danach fließt kein Strom mehr, die Spannung am Widerstand (schwarz) ist dann 0, die Spannung am Kondensator ist gleich der für t>0 konstanten Eingangsspannung (grün) von 1 Volt. |
Einschaltvorgang |
Im Laplace-Raum
Die Laplace-Transformation
|
Die (einseitige) Laplace-Transformierte einer Funktion f(t), mit f(t)=0 für t<0, ist gegeben durch: |
|
|
Die Laplace-Transformierte der Sinus- oder der Cosinus-Funktion sind etwa: |
|
|
Mit einer Laplace-Transformation lässt sich die Differentialgleichung mit konstanten Koeffizienten in eine algebraische Gleichung im Laplace-Raum überführen: |
|
|
Im Laplace-Raum sind Ausgabe und Eingabe einfach über eine rationale Übergangsfunktion verknüpft. |
|
|
Für den seriellen Schaltkreis mit der Differentialgleichung erhält man: |
|
|
|
|
Sinusförmige Eingangsspannung
Eine Lösung mit Xcos
|
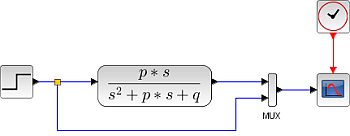
Mit dem Xcos-Block 'Continuous transfer function' hat man eine weitere Lösungsmöglichkeit des Problems an der Hand. |
|
|
Symbolische Xcos-Problemlösung mit Hilfe der Transferfunktion |
|
|
Der Spannungsverlauf für die Spannung am Kondenstor (schwarz) mit einer Anregungsfrequenz von diesmal ¼ ωr. |
|
Verrauscht - Eine Lösung mit 'csim'
|
'Weißes Rauschen' klingt nach alten Zeiten - nach dem Physikpraktikum im fünften Semester in den Katakomben der Uni Mainz. Da gab es Analogrechner und man musste stöpseln. |
|
|
Ui(t) = Ui0 sin(2π f1 t) + 'Weißes Rauschen'
Die Resonanzfrequenz des Schaltkreises ist Ua(t): |
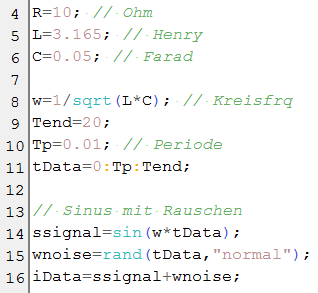
R=10; // Ohm L=3,165; // Henry C=0,05; // Farad f1=0,4; // Hertz Ui0=1; // Volt |
|
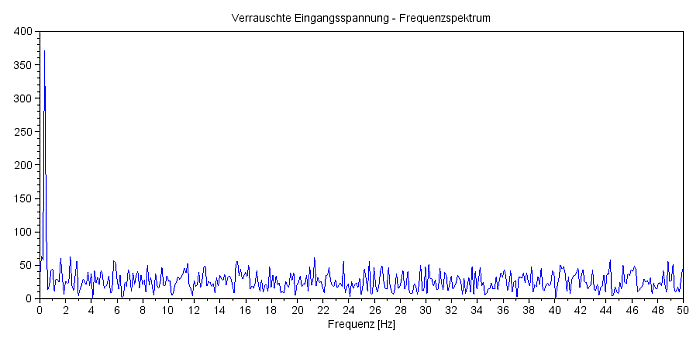
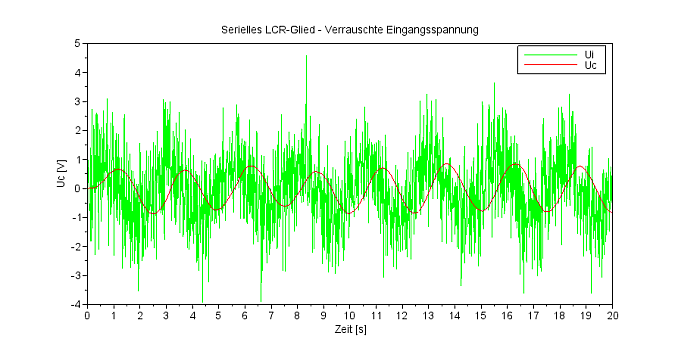
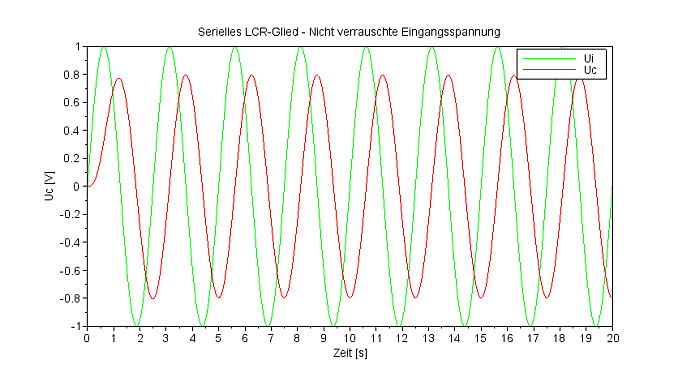
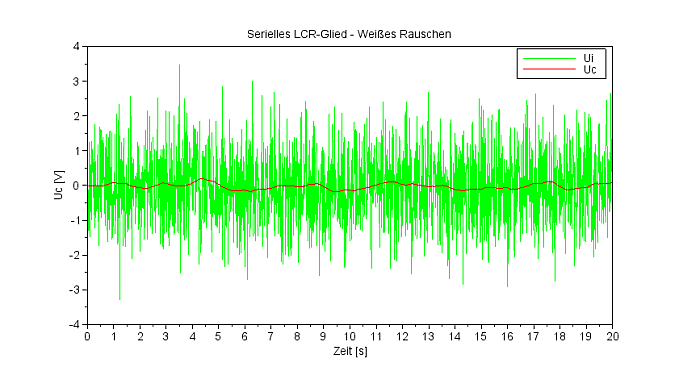
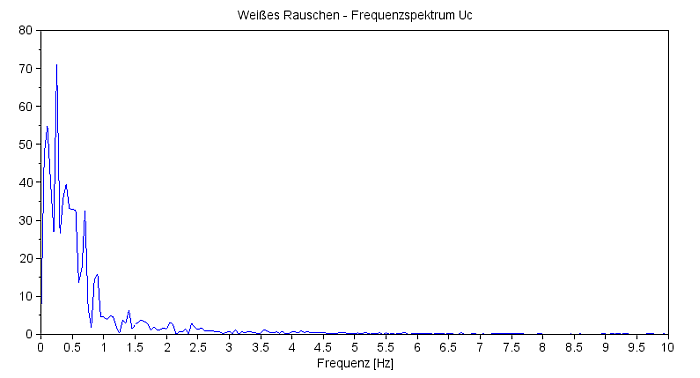
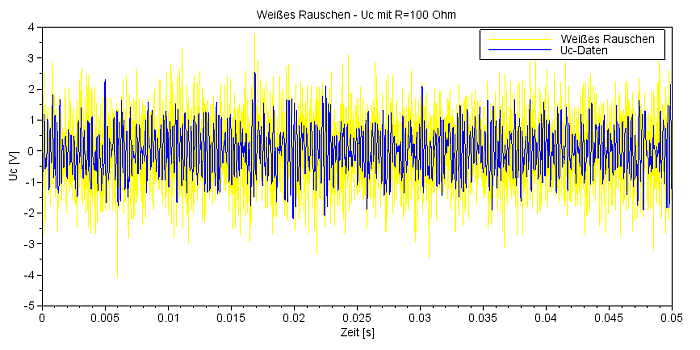
Zur Lösung wird die SciLab-Funktion 'csim' verwendet, als Vorlage kann das oben bebilderte csim-Beispiel verwendet werden. Dem reinen Sinus-Signal (Zeile 14) wird additiv weißes Rauschen 'wnoise' (Zeile 15) mit dem Mittelwert 0 und der Standardabweichung 1 hinzugefügt (Zeile 15), wie es der Code-Schnipsel zeigt. Das Diagramm zeigt die verrauschte Eingangsspannung (grün) und die geglättete Ausgangsspannung am Kondensator (rot). Das Frequenzspektrum zeigt in der Tat ein Rauschen mit einer Spitze bei 0,4 Hertz. |
Code-Schnipsel |
|
Frequenzspektrum des Eingangssignals |
|
|
Die Ausgangsspannung am Kondensator (rot)
|
|
|
Mich hat das Ergebnis durchaus überrascht, so dass ich schon an einen Fehler meinerseits gedacht habe. Daher habe ich für das nächste Diagramm das Rauschen herausgenommen und im übernächsten nur das Rauschen als Eingangsspannung verwendet und dazu noch des Frequenzspektum der Ausgangsspannung am Kondensator untersucht - die Ergebnisse sind plausibel. |
|
|
Die Ausgangsspannung am Kondensator (rot)
|
|
|
Die Ausgangsspannung am Kondensator (rot)
|
|
|
Das Frequenzspektrum der Ausgangsspannung am Kondensator
|
|
|
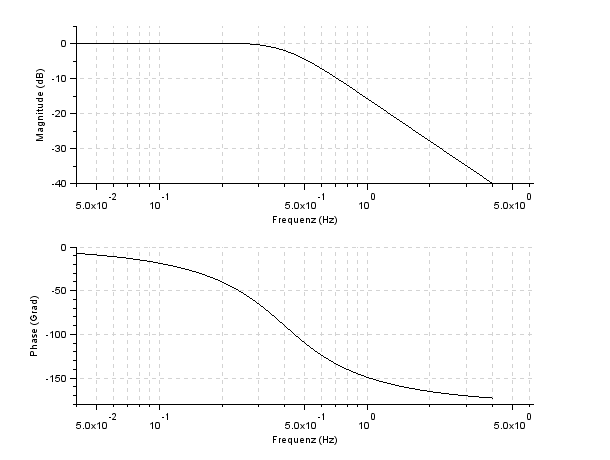
Im vorletzten Zeitdiagramm kaum zu erkennen! Wird dieser Schwingkreis mit weißem Rauschen gefüttert, so hat die Frequenzantwort, das Frequenzspektrum der Ausgangsspannung hier am Kondensator, bei der Resonanzfrequenz ein Maximum. Zum Vergleichen sei hier noch das Frequenzspektrum (und der Phasengang) gezeigt, wie er von SciLab mit der 'bode'-Funktion erzeugt wird. Es passt, ein breites Maximum und bei 5 Hz ist nichts mehr da ... |
|
|
Die beiden Bode-Diagramme, wie sie SciLab erzeugt |
|
|
|
Widerstand und Parallelschwingkreis in Reihe
Differentialgleichungen
|
|
|
|
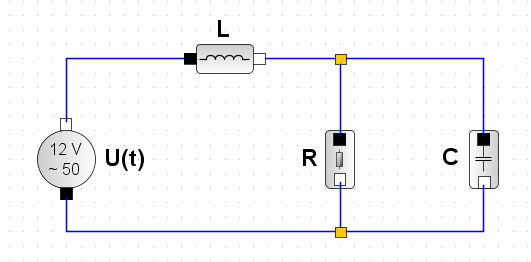
Die Kirchhoffschen Gesetze für elektrische Stromkreise verbinden die Ströme durch und die Spannungen an den Bauteilen des einfachen Schaltkreises. Die zeitabhängige Eingangsspannung ist Ui. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Sinusförmige Eingangsspannung
Die partikuläre Lösung
|
Der Schaltkreis wird mit der Anregungsfrequenz ω oszillieren, ich mache daher für die Spannung am Widerstand den einfachen Ansatz mit den beiden noch zu bestimmenden reellen Konstanten U0 und δ. |
|
|
|
|
|
|
|
|
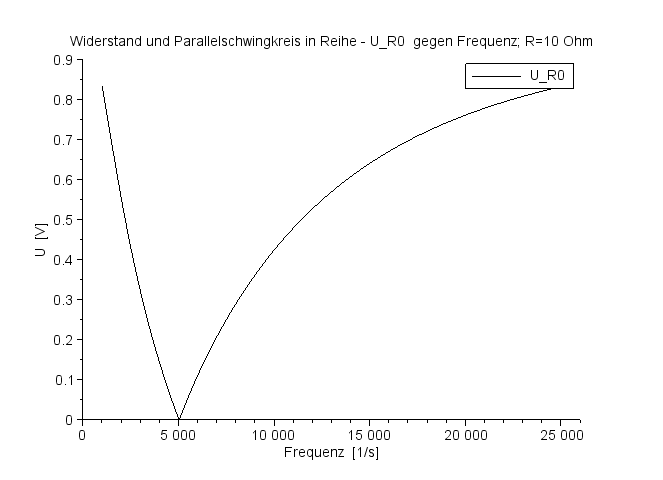
Die Amplitude der Spannung am ohmschen Widerstand ist eine Funktion der Anregungsspannung und verschwindet an der Resonanzfrequenz. |
|
|
Amplitudengang der Spannung am Widerstand bei R=10 Ohm |
|
Das vollständige Zeitverhalten
|
Ui(t) = Ui0 sin(ω t)
Die Resonanzfrequenz für den Schaltkreis ist Ua(t): |
R=10; // Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz Ui0=1; // Volt |
|
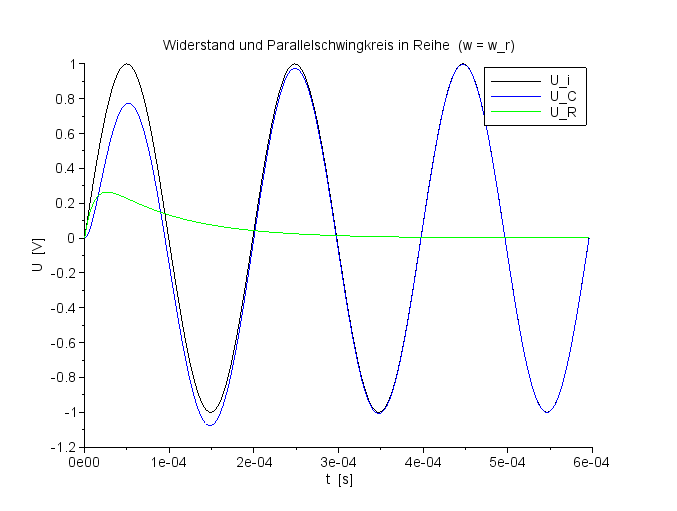
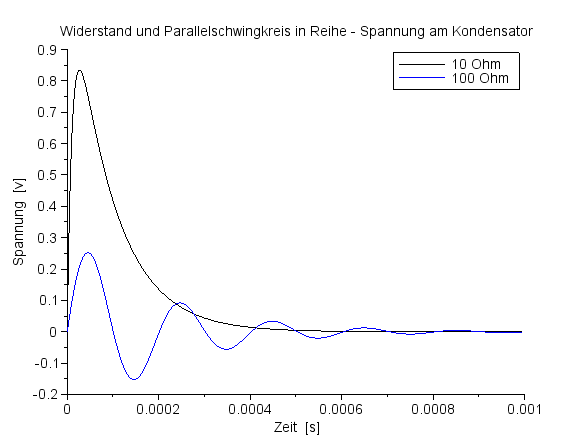
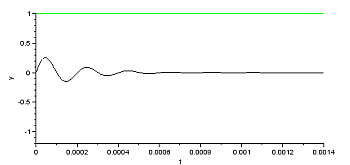
Ein prächtiges Diagramm! Im Resonanzfall kriecht die Spannung am Widerstand in wenigen Perioden gegen null, die gesamte Spannung liegt am Kondensator an. |
|
|
Spannungsverlauf für UC und UR bei f=ResFreq |
|
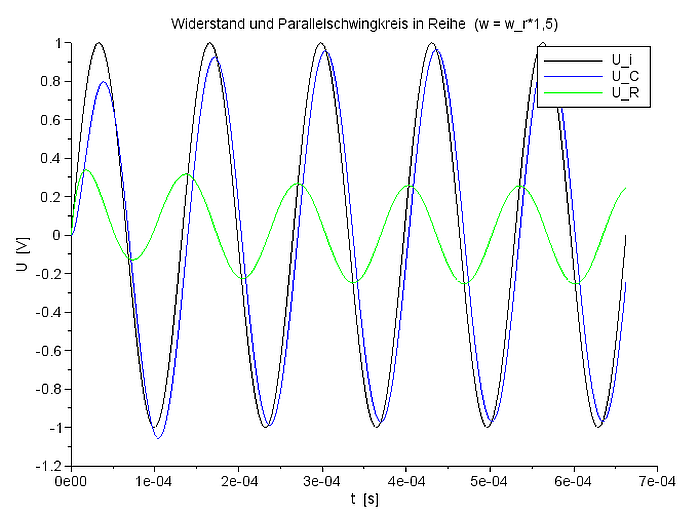
Spannungsverlauf für UC und UR bei f=ResFreq*1,50 |
|
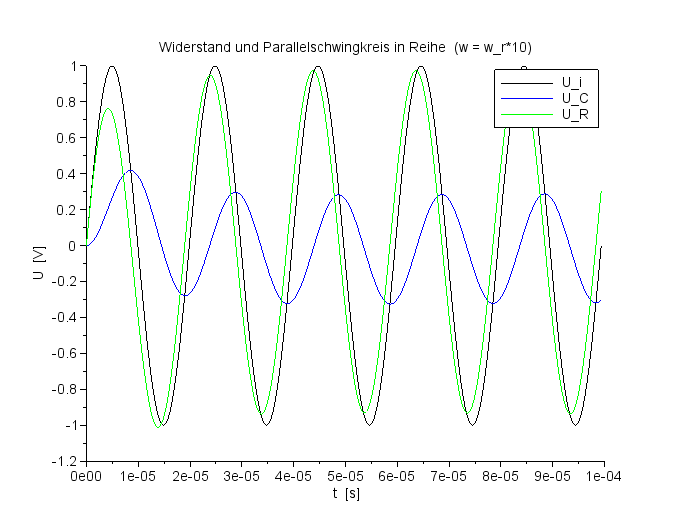
Spannungsverlauf für UC und UR bei f=ResFreq*10 |
|
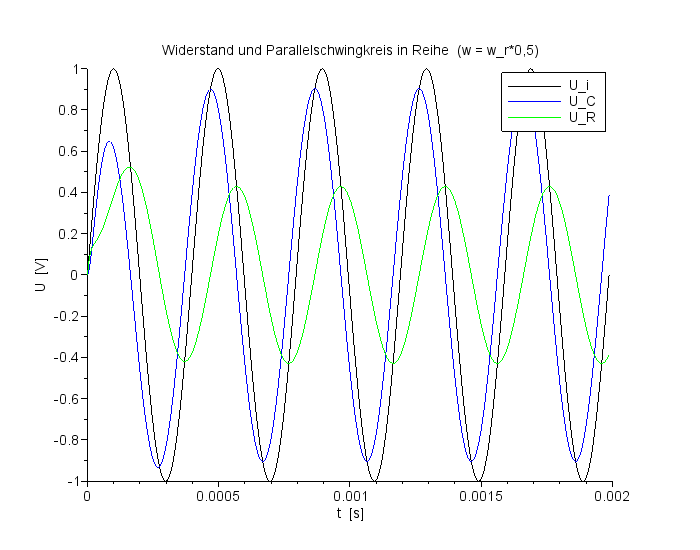
Spannungsverlauf für UC und UR bei f=ResFreq*0,50 |
|
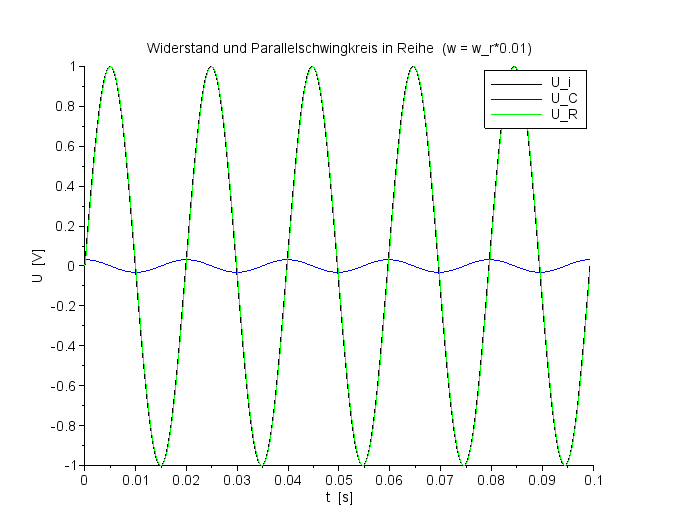
Spannungsverlauf für UC und UR bei f=ResFreq*0,01 |
|
Für kleine und große Frequenzen liegt also fast die gesamte Spannung am Widerstand, denn für kleine Frequenzen hat die Spule nur einen kleinen Scheinwiderstand (Impedanz) und umgekehrt hat der Kondensator für große Frequenzen nur eine kleine Impedanz. Sind Spule und Kondensator wie hier parallel verdrahtet, so kann für kleine und große Frequenzen über das LC-Glied nur eine kleine Spannung abfallen. |
Eine Lösung mit Xcos
|
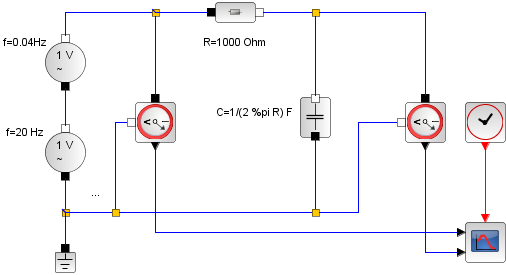
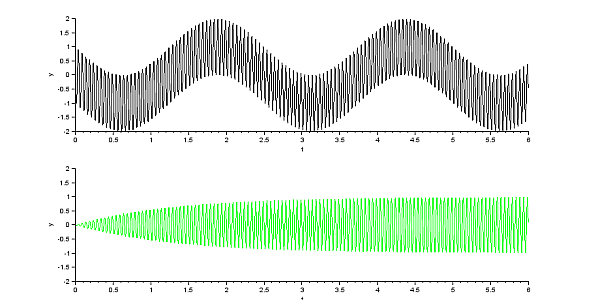
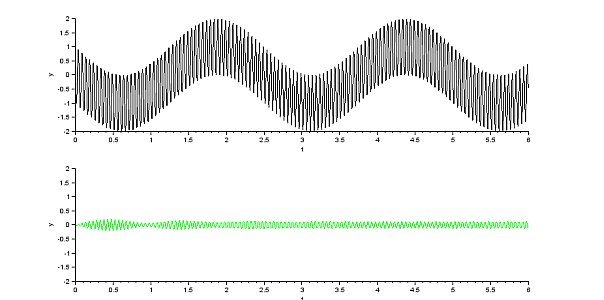
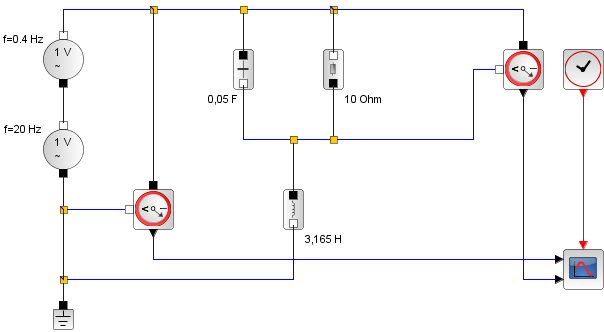
Hier noch die Simulation des Schaltkreises mit Xcos. Die Eingangsspannung setzt sich additiv aus 2 Anteilen unterschiedlicher Frequenz (20 und 0,4 Hertz) zusammen. Der Parallelschwingkreis ist zunächst auf die Resonanzfrequenz von 20 Hertz abgestimmt. Dann wird die Modulation des Signals mit 0,4 Hz herausgesiebt. Die Eingangsspannung ist schwarz gezeichnet, die Ausgangsspannung ist die Spannung an der Spule, sie ist in grün gezeichnet. Im zweiten Fall wird der Schwingkreis leicht verstimmt, die Werte für den Kondensator und die Spule werden um den Faktor 0,95 verkleinert. Die Ausgangsspannung bricht zusammen. |
|
Das Blockschaltbild |
|
Auf 20 Hz abgestimmter Schwingkreis |
|
Ein leicht verstimmter Schwingkreis |
Im Laplace-Raum
Übertragungsfunktion - Kondensator
|
|
|
|
Im Laplace-Raum sind Ausgabe und Eingabe einfach über eine rationale Übergangsfunktion verknüpft. |
|
|
Für (p2-4q)≠0 lässt sich mit den beiden Polstellen der Transfer-Funktion, s1 und s2, den Nullstellen des Nenner-Polynoms, die Funktion additiv aufspalten in zwei Summanden mit einfachen Polen. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Transfer-Funktion auf der imaginären Achse ist aufgespalten in Real- und Imaginärteil: |
|
|
|
|
|
|
|
|
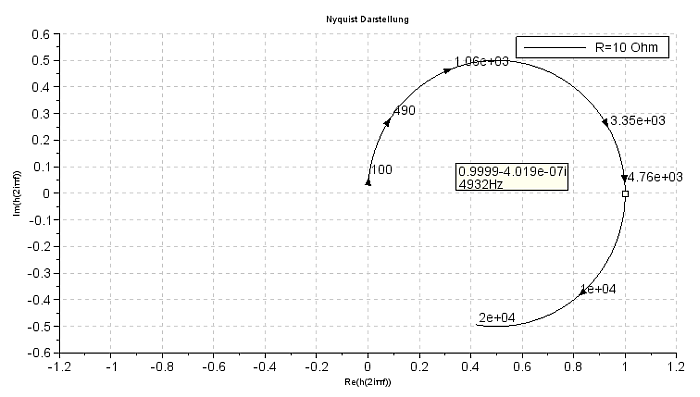
Die imaginäre Achse wird durch die Transfer-Funktion auf einen verschobenen Kreis mit dem Durchmesser 1 abgebildet – wie es das Nyquist-Diagramm unten auch zeigt. |
|
|
Der Betrag |Tia(i ω)| der Transferfunktion für s=iω ist:
|
|
|
Die Resonanzfrequenz für den Schaltkreis ist Tia(ω), T1a(ω): |
R=10; R=100; // Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz |
|
Polstellen für s/(2π) : R = 10 Ohm =>
|
- 14121,8 + 0,0 i - 1793,7 + 0,0 i |
|
Polstellen für s/(2π) : R = 100 Ohm =>
|
- 795,8 ± 4969,6 i |
|
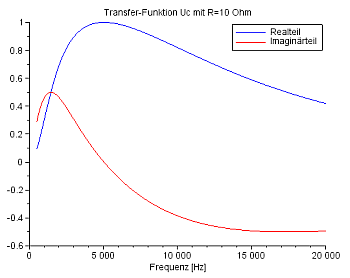
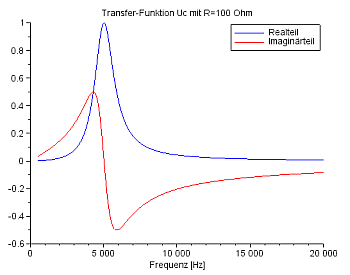
Die Transfer-Funktion für R=10 Ohm in Real- und Imaginärteil: |
Die Transfer-Funktion für R=100 Ohm in Real- und Imaginärteil: |
|
|
|
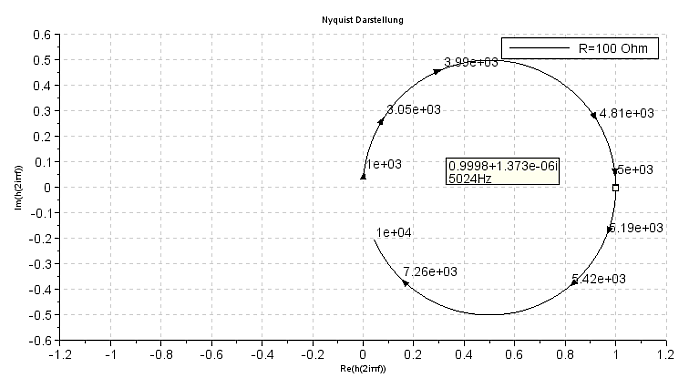
Nyquist-Diagramme für Tia(s) mit s= (2πi f) am Kondensator Die Nyquist-Diagramme von SciLab stellen Imaginärteil und Realteil der Transfer-Funktion in einer Ebene mit der Frequenz f als Parameter und s=(2πi f) dar. |
|
|
Nyquist-Diagramm für R=10 Ohm, f = 100 ... 20000 Hz |
|
|
Nyquist-Diagramm für R=100 Ohm, f = 1000 ... 10000 Hz |
|
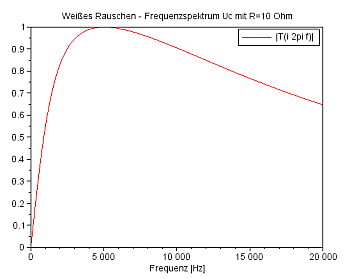
Der Betrag |Tia(i ω)| der Transferfunktion für s=iω stellt das Frequenzspektrum dar: |
|
|
Frequenzspektrum UC für R=10 Ohm |
Frequenzspektrum UC für R=100 Ohm |
Weißes Rauschen - Kondensator
|
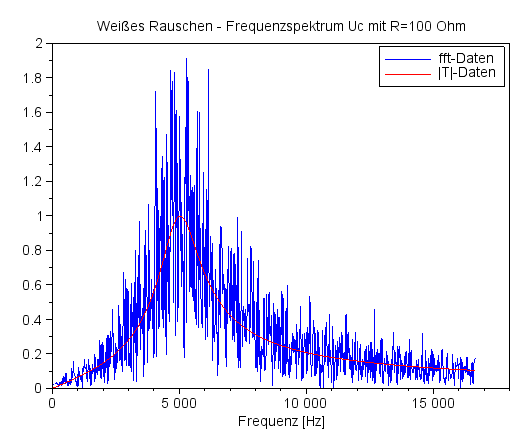
Ich möchte nun diese Frequenzgänge sozusagen experimentell ermitteln und füttere dazu den Schaltkreis mit Weißem Rauschen. Der Widerstand ist einmal 10 Ohm, das andere mal 100 Ohm. Die Ergebnisdaten der Frequenzanalyse mit Hilfe der SciLab-Funktion 'fft' habe ich mit dem Faktor 1/55=0,018 skaliert. |
|
|
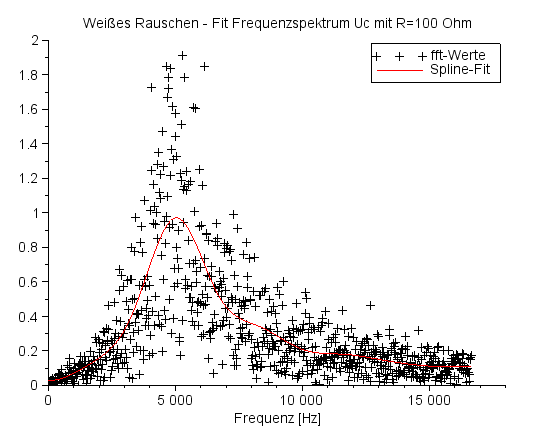
In Blau wird das gefilterte Rauschen präsentiert, die rote Kurve gibt den berechneten Frequenzgang wider. Das Rauschen ist passend skaliert. Ich bin überwältigt. |
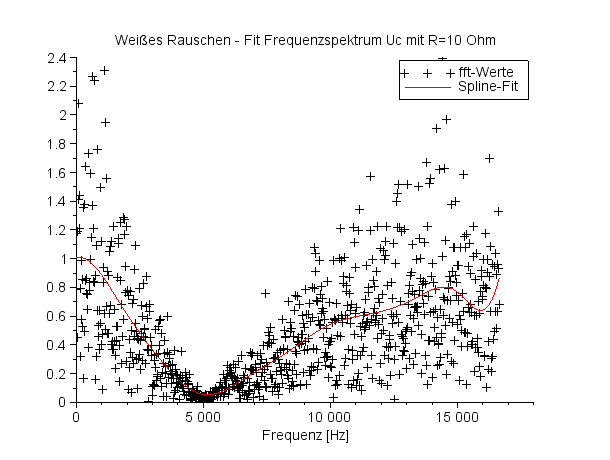
Die schwarzen Symbole '+' zeigen das gefilterte Rauschen an, die rote Kurve approximiert das Ergebnisrauschen über einen Spline-Fit mit 11 Stützpunkten ('weighted least squares cubic spline fitting'). |
|
Frequenzspektrum UC für R=10 Ohm |
Frequenzspektrum UC für R=10 Ohm |
|
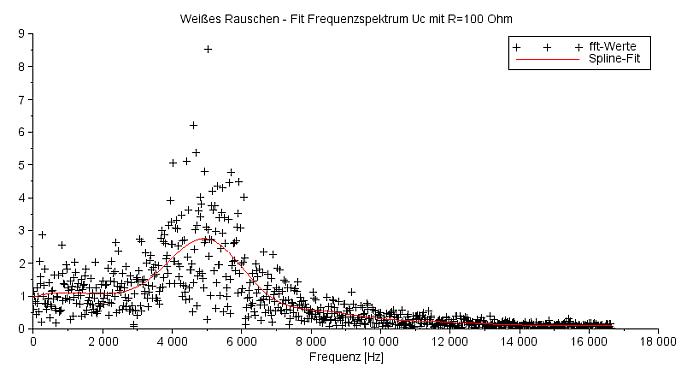
Frequenzspektrum UC für R=100 Ohm |
Frequenzspektrum UC für R=100 Ohm |
Weißes Rauschen - Widerstand
|
|
|
|
Im Laplace-Raum sind Ausgabe und Eingabe einfach über eine rationale Übergangsfunktion verknüpft. |
|
|
Der Betrag der Transferfunktion für s=iω ist dann:
|
|
|
Ui(t) = 'Weißes Rauschen'
Die Resonanzfrequenz für den Schaltkreis ist T1a(ω): |
R=10; R=100; // Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz |
|
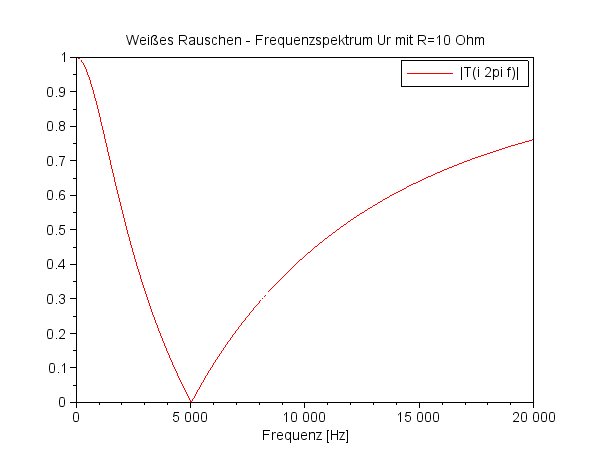
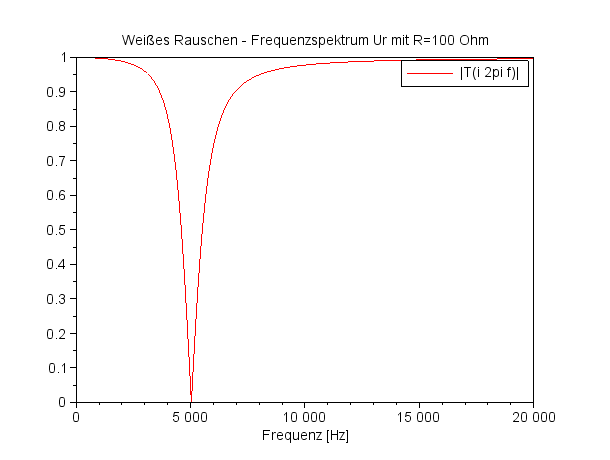
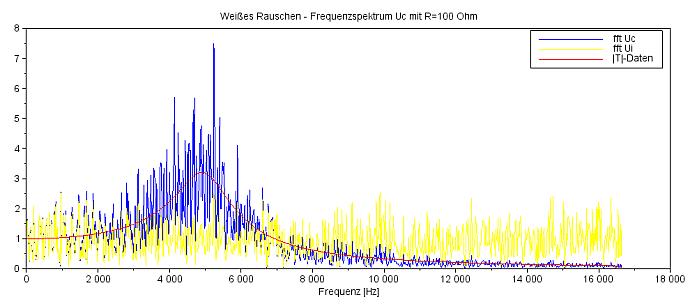
Frequenzspektrum UC für R=10 Ohm |
Frequenzspektrum UC für R=100 Ohm |
|
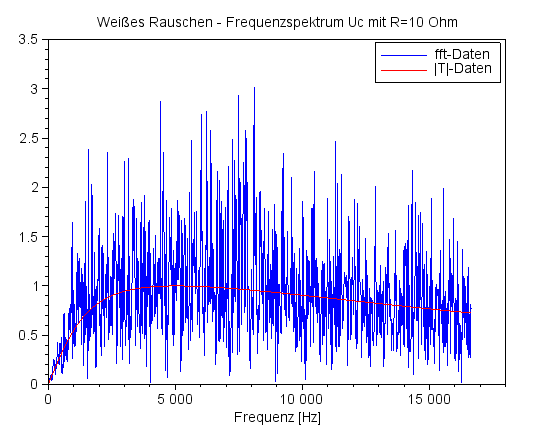
Ich möchte nun diese Frequenzgänge sozusagen experimentell ermitteln und füttere dazu den Schaltkreis mit Weißem Rauschen. Der Widerstand ist einmal 10 Ohm, das andere mal 100 Ohm. Die Ergebnisdaten der Frequenzanalyse mit Hilfe der SciLab-Funktion 'fft' habe ich mit dem Faktor 1/64=0,016 skaliert. |
|
|
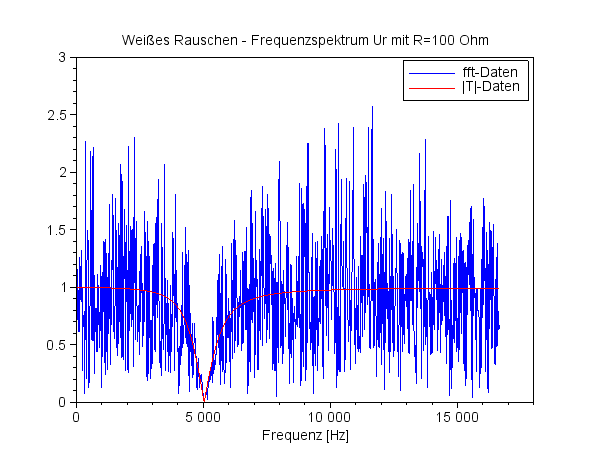
In Blau wird das gefilterte Rauschen präsentiert, die rote Kurve gibt den berechneten Frequenzgang wider. Das Rauschen ist passend skaliert. |
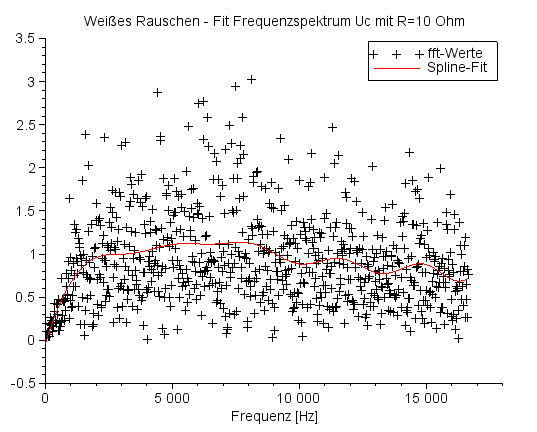
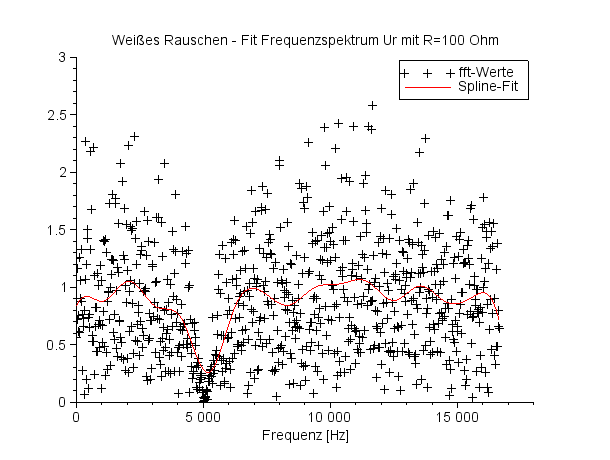
Die schwarzen Symbole '+' zeigen das gefilterte Rauschen an, die rote Kurve approximiert das Ergebnisrauschen über einen Spline-Fit mit 17 Stützpunkten ('weighted least squares cubic spline fitting'). |
|
Frequenzspektrum UC für R=10 Ohm |
Frequenzspektrum UC für R=10 Ohm |
|
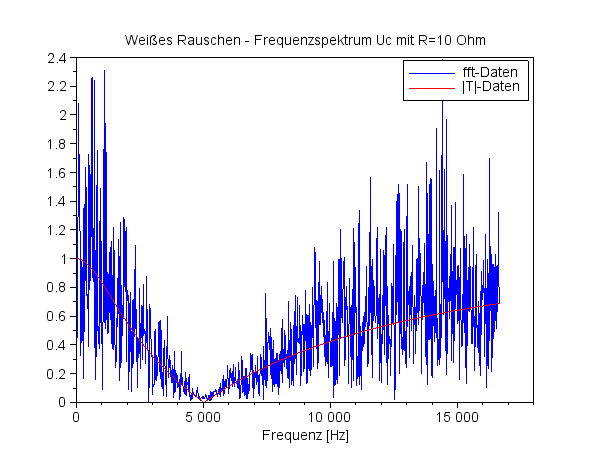
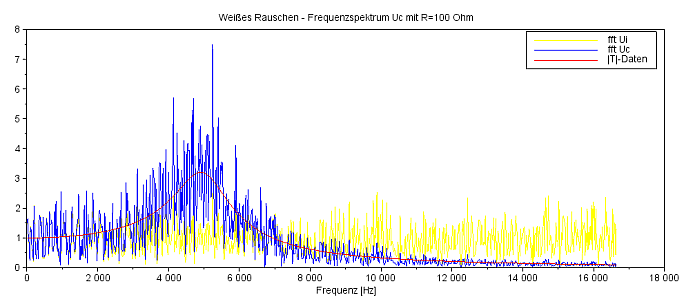
Frequenzspektrum UC für R=100 Ohm |
Frequenzspektrum UC für R=100 Ohm |
|
Für die Spitze scheint die Fit-Methode nicht so geeignet zu sein. |
|
Der einfache Einschaltvorgang - berechnet
|
Die Transfer-Funktion für die Spannung am Kondensator (UC=Ua) ist: |
|
|
Wird eine für t>t0 konstante Spannung von 1V zur Zeit t0 eingeschaltet, lässt sich dies durch eine Stufenfunktion im Zeitenraum beschreiben. Deren Laplace-Transformierte ist gegeben durch: |
Θ(t) = 0 für t<0, Θ(t) = 1 für t>0
|
|
Die Spannung am Kondensator wird dann durch Ûa beschreiben, wenn man die Eingangsgröße Ûi ersetzt: |
|
|
Spaltet man die rationale Funktion nach den Polen s1 und s2 auf, erhält man: |
|
|
Ich nehme an, das s1 und s2 in der linkem, negativen Halbebene liegen. Die Spannung im Zeitenraum erhält man durch die inverse Lapace-Transformation. |
|
|
Der Integrationsweg verläuft zunächst über die vertikale Strecke von (t0 - i R) nach t0 + i R). Für t< t0 wird der Integrationsweg über einen Halbkreisbogen HKR mit dem Radius R in der rechten Halbebene geschlossen. In dem so definierten Gebiet G liegen keine Pole, der Integrand ist in dem Gebiet holomorph (komplex differenzierbar). |
|
|
Nach dem Cauchy'schen Integralsatz verschwindet dann das Wegintegral über den Rand δG dieses Gebietes. Es gilt daher:
|
|
|
Der Integrationsbeitrag des Halbkreises mit dem Radius R verschwindet mit dem Faktor e-Rt. Für R → ∞ erhält man die Spannung am Kondensator für t<t0 zu: |
|
|
Für t>t0 wird der Integrationsweg über einen Halbkreisbogen HKR mit dem Radius R in der linken Halbebene geschlossen. In dem so definierten Gebiet G liegen zwei Pole. Den Rand dieses Gebietes G deformiert man nun so, dass die Pole von kleinen Kreisen fast umschlosssen sind und außerhalb des Gebietes zu liegen kommen. |
|
|
Links im Beispiel ist der anfängliche Integrationsweg für einen Pol aufgezeichnet. Im Innern des so entstandenen Gebietes liegen keine Pole, der Integrand ist in diesem Gebiet holomorph, das Wegintegral über den Rand des Gebietes verschwindet wieder. Das gesuchte Integral über die vertikale Strecke hat dann drei Beiträge. Der Beitrag des großen Halbkreisbogens verschwindet im Falle t>t0 für große R. Die beiden Wege hin und weg von den Polen werden in unterschiedlicher Richtung durchlaufen und heben sich im Grenzfall auf, wenn nämlich die Radien der kleinen Kreise gegen 0 geht. |
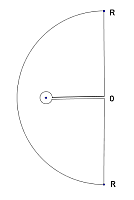
|
|
Es bleibt der Beitrag der kleinen Kreise kl um die Pole, die im Grenzfall jeweils einen Pol umschließen. Und hier gibt es die Beiträge, die nicht verschwinden, denn es sind die Polstellen, die für komplexe Funktionen bei der Integration eine Rolle spielen – gleich ein Beispiel dazu. |
|
|
Das Wegintegral um den Polstelle z=0 verschwindet nicht! Γ ist hier ein kleiner Kreis um den Nullpunkt der komplexen Ebene. |
|
|
Damit kann man im Grenzfall das gewünschte Integral wunderbar einfach berechnen. Man beachte: die kleinen Kreise werden im Uhrzeigersinne durchlaufen – deshalb gibt es hier ein Minuszeichen.
|
|
|
|
|
|
Die resultierenden Anfangsbedingungen sind: |
|
|
|
|
|
|
|
|
Ausgangsspannungen beim Einschaltvorgang UI=Θ(t) |
|
|
Die Eingangsspannung hat ja für t=t0 eine Unstetigkeitsstelle, hier ist noch etwas Forschung vonnöten, auch was die möglichen additiven Terme angeht, die bei der Transformation der Differentialgleichungen in algebraische Gleichungen auftreten können. |
|
Der einfache Einschaltvorgang – mit Xcos
|
Die experimentelle Überprüfung der inversen Laplace-Transformation ist angesagt – mit einem Xcos-Blockdiagramm ist das schnell erledigt. Die Eingangsspannung wird zur Zeit t0=0 eingeschaltet und macht einen sehr schnellen Sprung auf 1V, sie bleibt für t>0 dann konstant auf 1V. Das Ergebnis passt zu den Rechnungen ... |
|
|
Der Einschaltvorgang mit R=10 Ohm. |
Der Einschaltvorgang mit R=100 Ohm. |
|
|
|
|
Die Ausgangsspannung am Kondensator ist schwarz gezeichnet. Für kleine Widerstände ist der anfängliche Anstiegswinkel für t≈0 fast 90°, für größere Widerstände, etwa 1000 Ohm, nähert er sich der Null. |
|
|
|
Ein passiver Tiefpass-Filter
Differentialgleichungen
|
|
|
|
Die Kirchhoffschen Gesetze für elektrische Stromkreise verbinden die Ströme durch und die Spannungen an den Bauteilen des einfachen Schaltkreises. Die zeitabhängige Eingangsspannung ist Ui. |
|
|
|
|
|
|
|
Sinusförmige Eingangsspannung
Das vollständige Zeitverhalten
|
Ui(t) = Ui0 sin(ω t) Die Resonanzfrequenz für den Schaltkreis ist 5033 Hertz. Ua(t): |
R=10; // Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz Ui0=1; // Volt |
|
Spannungsverlauf für UR und UL bei f=ResFreq |
|
|
Spannungsverlauf für UR und UL bei f=ResFreq*1,5 |
|
|
Spannungsverlauf für UR und UL bei f=ResFreq*0,50 |
|
Zweifachfrequenzantrieb
|
Ui(t) = Ui0 sin(2π f1 t) + Ui0 sin(2π f2 t) Die Resonanzfrequenz für den Schaltkreis ist 0,4 Hertz. Ua(t): |
R=10,0; // Ohm L=3,165; // Henry C=0,05; // Farad ResFreq=0,4; // Hertz Ui0=1; // Volt f1=20,0; // Hertz f2=0,4; // Hertz |
|
Xcos-Blockschaltbild |
|
|
Spannungsverlauf für Ui und UR (blau) |
|
Im Laplace-Raum
Weißes Rauschen - Kondensator
|
|
|
|
Man erhält die Transfer-Funktion; |
|
|
Ersetzt man in der Transferfunktion 's' durch 'iω' und geht damit in den Fourier-Raum, so lässt sich die 'Frequenzantwort ', das ist Betrag und Phase der Transferfunktion, ermitteln. |
|
|
Die SciLab-Funktion 'bode' gibt gleich die beiden Diagramme recht ingenieursmäßig aus.
Weißes Rauschen mit der Amplitude 1 lässt sich durch
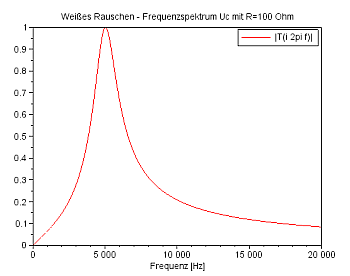
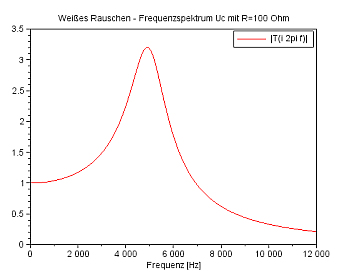
Das Diagramm rechts sollte die Frequenzantwort auf Weißes Rauschen für einen Widerstand von 100 Ohm darstellen, gegeben durch |T(iω)|: |
|
|
Ui(t) = 'Weißes Rauschen' Die Resonanzfrequenz für den Schaltkreis ist 5033 Hertz. UC |
R=10; R=100;// Ohm L=1,0E-3; // Henry C=1,0E-6; // Farad ResFreq=5033; // Hertz |
|
Spannungsverlauf für Ui (Weißes Rauschen, gelb) und UC (blau) |
|
|
Man erkennt zwar eine filternde Wirkung, ansonsten bleibt die Art der Wirkung offen. Da kann nur ein Bummel durch den Frequenzraum helfen. Die beiden nächsten Diagramme zeigen dieselben Informationen, das Frequenzspektrum für die Eingangsspannung und die Spannung am Kondensator. Nun erkennt man den Buckel um die Resonanzfrequenz und die Dämpfung im hohen Frequenzbereich. |
|
|
Frequenzspektrum (Ia) für Ui (Weißes Rauschen, gelb) und UC (blau) |
|
|
Frequenzspektrum (Ib) für Ui (Weißes Rauschen, gelb) und UC (blau) |
|
|
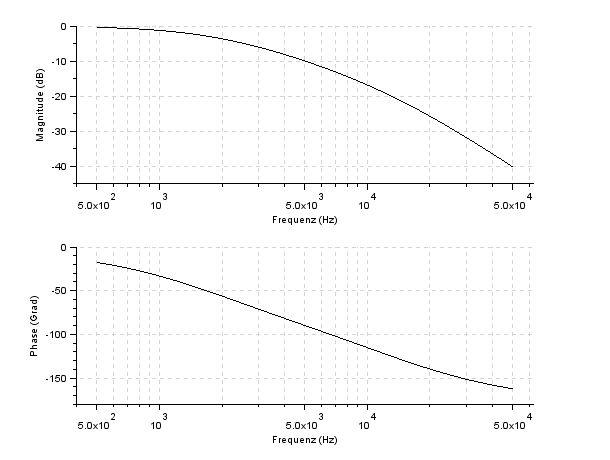
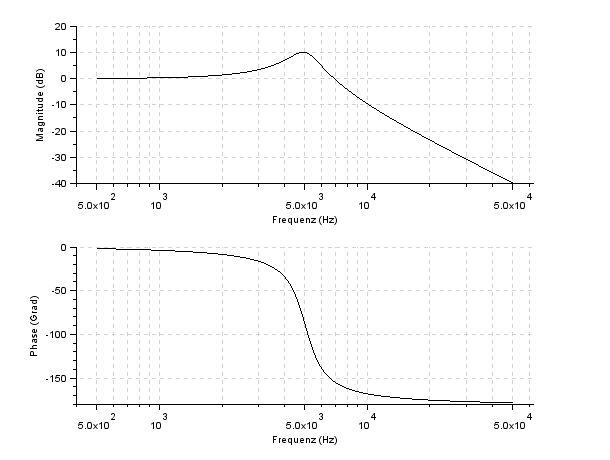
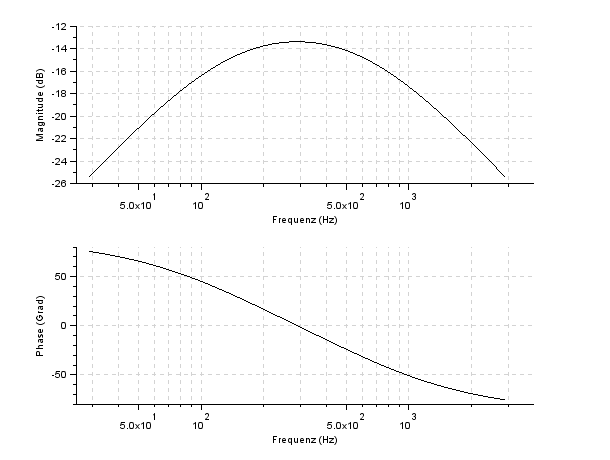
Unten sind die Bode-Diagramm von SciLab jeweils für einen Widerstand von 10 und 100 Ohm zu sehen. Für den größeren Widerstand ist der Verlauf markanter. Beachten Sie: Die Abszisse trägt einen logarithmischen Maßstab. Und 'dB' mag ich schon gar nicht. Aber immerhin kann man den Buckel erkennen ... |
|
|
Spektrum und Phasengang für R=10 Ohm |
|
|
Spektrum und Phasengang für R=100 Ohm |
|
|
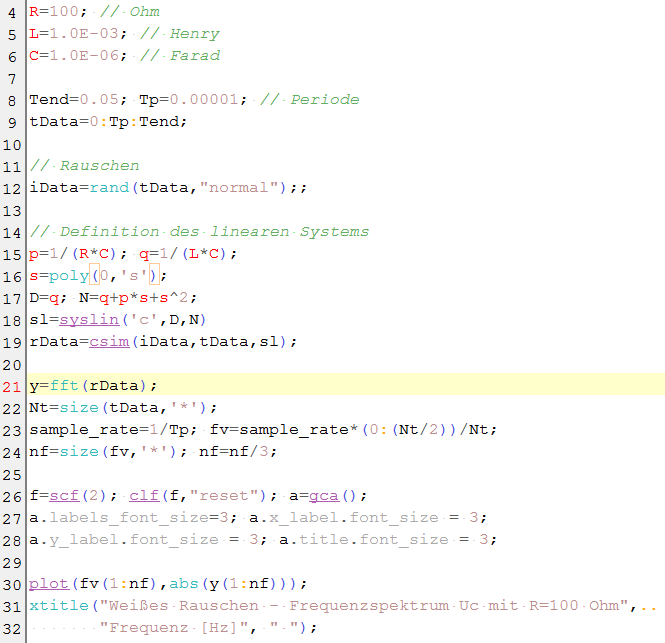
Für den Widerstand von 100 Ohm soll nun noch, um vergleichen zu können, sozusagen experimentell das Frequenzspektrum mittels Weißem Rauschen ermittelt werden. Den vollständigen SciLab-Quellcode finden Sie abgebildet.
Ich belasse es mehr oder weniger bei einem qualitativen Vergleich per Inaugenscheinnahme. |
|
|
SciLab-Code für das Frequenzspektrum |
|
|
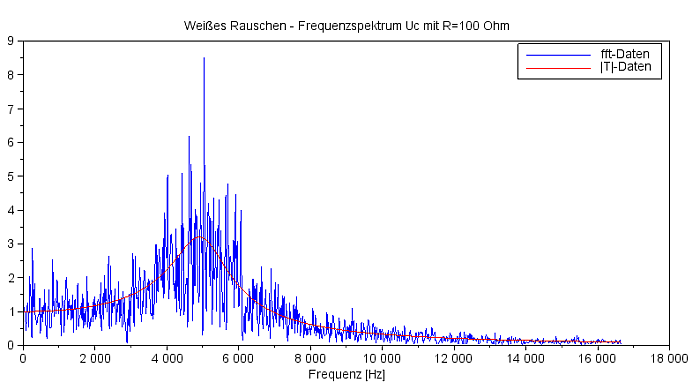
Das Frequenzspektrum für Uc mit Weißem Rauschen (R=100 Ohm) |
|
|
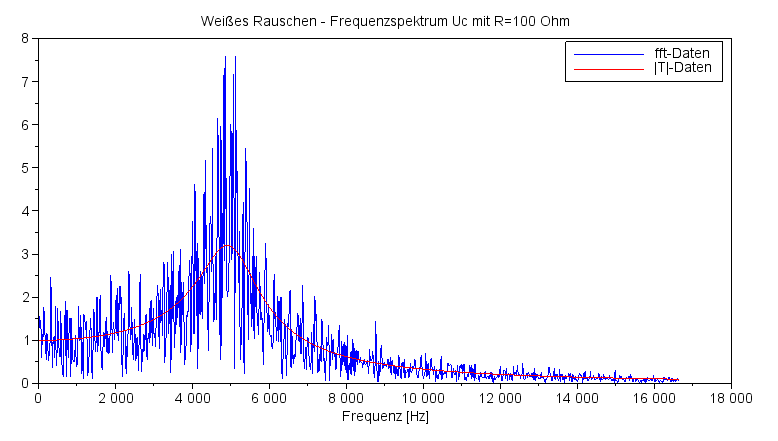
Die Werte für das Frequenzspektrum (blau), die die SciLab-Funktion zurückgibt, habe ich mit dem Faktor 1/(2 |T|3max) (das ist ungefähr der Faktor 2*3,23=0,015) skaliert. Die rote Kurve gibt den (berechneten) Verlauf für das Spektrum |T|1 (kein Quadrat) wieder. Das gefilterte, skalierte Weiße Rauschen ('+') habe ich durch eine Spline- Kurve (mit 11 Stützpunkten) angenähert. Immerhin, sie startet bei einem Wert knapp über die 1 und ihr Maximalwert liegt an der Resonanzfrequenz bei dem Wert 3,2, aber ganz zufriedenstellend ist der Vergleich nicht – hier muss noch in fachlicher Hinsicht und beim Thema SciLab nachgebessert werden. |
|
|
Ein Fit für das Frequenzspektrum (R=100 Ohm) mit |
|
|
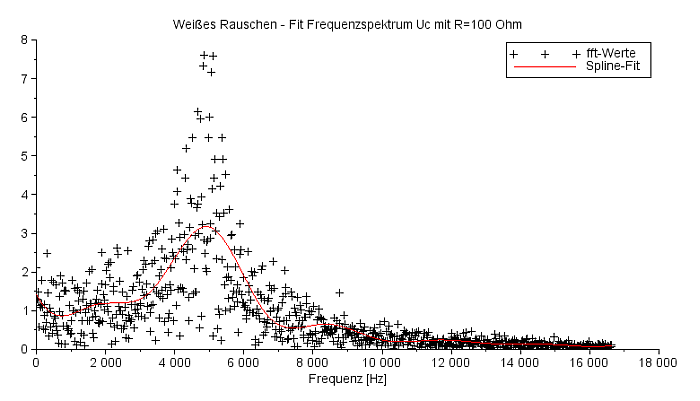
Das von SciLab erzeugte Weiße Rauschen unterliegt natürlich einem (Pseudo-)Zufallprozeß - um dieses zu bebildern, ein weiteres 'Experiment' mit dem Rauschen. Die Übereinstimmung ist doch so schlecht nicht. |
|
|
Das Frequenzspektrum für Uc mit Weißem Rauschen (R=100 Ohm) |
|
|
Ein Fit für das Frequenzspektrum (R=100 Ohm) mit |
|
|
|
Kein Schwingkreis – Ein Bandpass-Filter
|
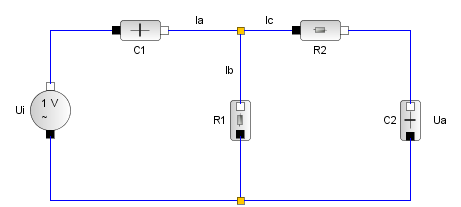
Schaltbild des Bandpass-Filters |
||
|
|
|
|
|
|
|
|
|
Kleinbuchstaben indizieren die Ströme im Bandpass-Filter, Großbuchstaben stehen für die Bauteile des Schaltkreises und für die Ströme durch die Bauteile. Das spitze Dach kennzeichnet die Laplace-Transformierte. |
||
Im Laplace-Raum
|
Ich suche einen schnellen, algebraischen Lösungsansatz, der sich systematisch anwenden lässt. Habe ich erst einmal die Übertragungsfunktion im Laplace-Raum, so lässt sich mit Scilab alles damit machen, was man sich wünschen kann. Naja. |
|
|
Die Kirchhoffschen Regeln sind leicht anzuwenden und ergeben die drei Bestimmungsgleichungen für die drei Ströme Ia, Ib, Ic: |
|
|
Die Bestimmungsgleichungen transformiere ich in den Lapalce-Raum und schreibe sie um im eine Matrix-Gleichung. Die Matrix nenne ich M. Ihre Determinante ist det M oder auch |M|. |
|
|
|
|
|
Die Matrix ließe sich invertieren, dann erhielte man alle drei Ströme, ich möchte die Cramersche Regel anwenden und brauche zuerst die Determinante: |
|
|
|
|
|
Die Cramersche Regel lässt sich leicht merken, ich möchte die Lösung für die 3. Komponente berechnen und ersetze dazu die 3. Spalte in der Matrix M durch den Inhomogenitätsvektor (das ist die linke Seite der Matrix-Gleichung). Wunderbar. |
|
|
Die Transferfunktion von der Eingangsgröße zur Ausgangsgröße am Kondensator C2 ergibt dann in einer kleinen, angenehmen Rechnerei:
|
|
|
Und es braucht nur einige, wenige Zeilen Code, damit SciLab das lineare System beleben kann! Die Zeilen 17-19 legen die Koeffizienten der Polynome fest, die Zeile 22 definiert Zähler- und Nenner-Polynom der rationalen Funktion, die Zeile 23 macht das lineare System auch SciLab zugänglich und in Zeile 24 findet man bereits das gefilterte Rauschen wieder. |
|
|
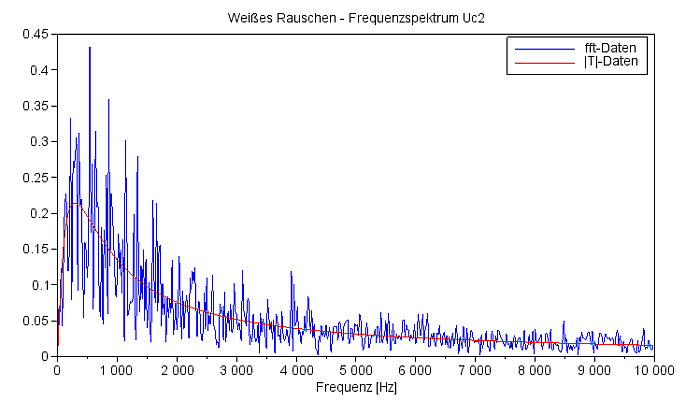
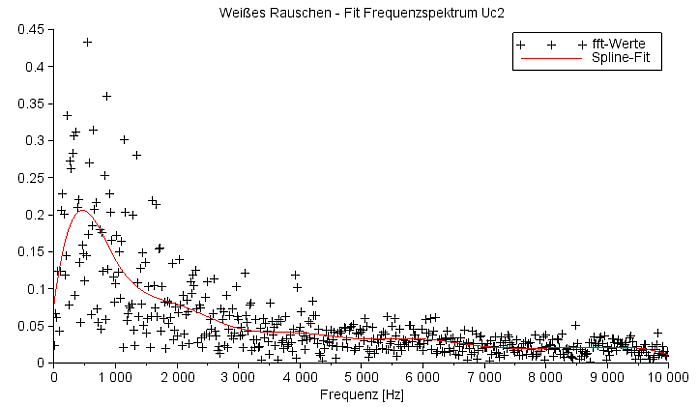
Ui(t) = 'Weißes Rauschen' Das Maximum des Spektralverlaufes liegt bei knapp 300 Hz. Tia(t): |
R1=100; // Ohm R2=1000; // Ohm C1=3,0E-6; // Farad C2=1,0E-6; // Farad |
|
Frequenzspektrum UC2 |
|
|
Frequenzspektrum UC2 |
|
|
Die Güte eines Filters hängt von der gewünschten Breite des Bandes und der Steilheit der Flanken ab. Das ist aber eine Angelegenheit der Signalverarbeitung und der Regelungstechnik. SciLab bietet einige Unterstützung beim Entwerfen von Filtern. Der Vollständigkeit halber sei noch das schnöde Bode-Diagramm, wie es SciLab erzeugt, nachgeschoben. Der Frequenzbereich geht hier nur bis 3000 Hz. |
|
|
Das Bode-Diagramm für den Schaltkreis |
|
|
|
Anhang
Lineare Differentialgleichungen 2. Ordnung
mit konstanten Koeffizienten
|
Die obigen Differentialgleichungen zweiter Ordnung haben die Form: |
|
|
p und q sind Konstante. f(t) ist eine gegebene stetige Funktion in der Zeit. Das Anfangswertproblem für diese DGL ist eindeutig lösbar. Die Lösung setzt sich aus einer Lösung Yh der homogenen DGL mit f(t)≡0 und einer partikulären Lösung Yp zusammen. |
|
|
Homogene Lösung: Setzt man für die homogene Lösung einen Exponentialansatz an, erhält man die charakteristische Gleichung, die die homogenen Lösungen bestimmen. |
|
|
Aperiodischer Kriechfall: Die charakteristische Gleichung hat 2 reelle Lösungen ω1 und ω2. |
|
|
Aperiodischer Grenzfall: Die charakteristische Gleichung hat 1 reelle Lösung ω. |
|
|
Schwingungsfall – gedämpft und ungedämpft: Die charakteristische Gleichung hat 2 zueinander konjugiert komplexe Lösungen ω und ω*. Für p=0 ist die Schwingung ungedämpft. |
|
|
Partikuläre Lösung: Die partikulären Lösung erhält man eine sogenannte Variation der Konstanten. Dazu geht man von einem multiplikativen Ansatz für die partikuläre Lösung aus – ausgehend von 2 bekannten, linear unabhängigen Lösungen der homogenen DGL. |
|
|
Die beiden Funktionen g1(t) und g2(t) sind so zu bestimmen, dass Yp die inhomogene DGL erfüllt. |
|
|
Als allgemeine Lösung erhält man damit: Die Konstanten sind aus den Anfangsbedingungen zu berechnen. |
|
Aufbereitung der Differentialgleichung für den ODE-Löser
|
Die obigen Differentialgleichungen zweiter Ordnung haben die Form: |
|
|
p und q sind Konstante. f(t) ist eine gegebene Funktion in der Zeit. Um diese Gleichung mit Hilfe von SciLab lösen zu können, muss diese Differentialgleichung in zwei Differentialgleichungen erster Ordnung überführt werden. Dazu wird eine Hilfsvariable Y eingeführt: |
|
|
Mit |
|
|
Der DGL-Löser von SciLab erhält seine Informationen über einen hier zweidimensionalen Zustandsvektor: |
|
|
Die zu lösende DGL wird dem DGL-Löser als Funktion übergeben, die Funktion berechnet die Werte für die Ableitungen und gibt diese als Paar zurück: |
|
Lineare zeitlich-kontinuierliche Systeme im Zustandsraum
|
Ein System S werde durch einen Zustandsvektor x beschrieben. Angetrieben durch einen Vektor von Eingangsgrößen ui verändert sich das System zeitlich in linearer Weise. |
|
|
Die Änderung des Zustandsvektors wird durch 2 Matrizen A und B beschrieben, die Matrix A ist quadratisch. |
|
|
Ein Beobachter B misst einen Satz von Ausgangsgrößen yB, die Ausgangsgrößen sollen in einem linearen Zusammenhang mit dem Systemzustand und den Eingangsgrößen stehen. |
|
|
Solche System lassen sich mit dem SciLab Xcos-Block CLSS (Continuous State-Space System) erfassen. |
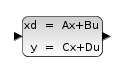
|
|
Über eine Variation der Konstanten lässt sich auch eine geschlossene Lösung angeben: |
|
Die Laplace-Transformation und mehr
|
Eine im Definitionsbereich stückweis stetige Funktion sei für alle t∈[0,∞) nach oben durch zwei Konstanten a und M beschränkt: |
|
|
Die (einseitige) Laplace-Transformierte der Funktion f(t) existiert dann für alle s > a: |
|
|
Eigenschaften |
|
|
Mittels einer partiellen Integration erhält man die Laplace-Transformierte der zeitliche Ableitung einer Funktion zu: |
|
|
Und für die zweite Ableitung gilt weiter: Ähnliches gilt für höhere Ableitungen. |
|
|
Und für das Integral einer exponential-beschränkten Funktion f gilt: |
|
|
Die Faltung zweier geeigneter Funktion f und g ist definiert durch: Die Laplace-Transformierte der gefalteten Funktionen ist dann: |
|
|
Die Exponentiation führt zu einer Translation im Faltungsraum. |
|
|
Rücktransformation |
|
|
Die Rücktransformation erhält man mit einem Integral entlang einer vertikalen Kontour in der komplexen Ebene. |
|
|
Die reelle Zahl c ist so zu wählen, dass alle Singularitäten zur Linken oder zur Rechten des Integrationsweges liegen. Der Integrationsweg wird in aller Regel durch einen großen Kreis im Unendlichen geschlossen, womit sich der Residuensatz der Funktionentheorie anwenden lässt. |
|
|
Beispiele |
|||||
|
Ein einfacher Einschaltvorgang zur Zeit t0 kann durch die Stufenfunktion beschreiben werden: 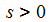
|
|
||||
|
|
|
||||
|
Beispiele für einfache Laplace-Transformationen sind: Die Funktion Γ ist eben die Gamma-Funktion, die für eine natürliche Zahl n ihre Fakultät liefert: Γ(n+1)=n!. |
|||||
|
|
||||
|
|||||
|
|||||
|
Und mehr ... |
|
|
Eine nahe Verwandte der (zweiseitigen) Laplace-Transformation ist die Fourier-Transformation. |
|
|
Für eine geeignete Funktion f ist die Fourier-Transformation definiert durch: |
|
|
Eine weitere Funktion ist die Diracsche Delta-Funktion δ(x-a), sie kam erst spät als Distribution zu mathematischen Ehren, sie ist definiert durch: |
|
|
Dieses Delta-Gebilde lässt sich in verschiedenen Formen ausschreiben: |
|
|
Oder auch als die Fourier-Transformierte der identischen 1-Funktion: |
|
|
Die Delta-Funktion stellt zeitlich gesehen einen kurzen Impuls dar. Im Frequenzraum ist das eine Überlagerung aller Frequenzen mit gleicher Amplitude – eben Weißes Rauschen. |
|
Etwas Funktionentheorie – Der Residuensatz
|
Eine in einem Gebiet G definierte komplexe Funktion f heißt an der Stelle z0 komplex differenzierbar, wenn a Häufungspunkt von G ist und die Ableitung f'(a) als Grenzwert existiert: |
|
||
|
Der schnelle Weg – die Funktion f ist an Stelle z0 komplex differenzierbar, wenn dort gilt: |
|
||
|
Die Funktion heißt in dem Gebiet G holomorph, wenn f in jeden Punkt von G komplex differenzierbar ist. |
|||
|
Ist G ein einfach-zusammenhängendes Gebiet und ist die Funktion f in G holomorph, so gilt für jede in G gelegene einfach-geschlossene Kurve γ: |
|
||
|
Das Integral von Anfangs- zum Endpunkt einer Kurve ist damit unabhängig vom Verlauf der Kurve (Wegunabhängigkeit). |
|||
|
Ist f in einer punktierten Umgebung von z0 holomorph und ist γ eine z0 umschließende einfach-geschlossene Kurve mit positivem Umlaufsinn, so heißt (res f)(z0) Residuum von f an der Stelle z0: |
|
||
|
Der schnelle Weg – das Residuum einer Funktion f an Stelle z0 ist: |
|
||
|
Auch ein schneller Weg und zugleich eine Erklärung für den ersten schnellen Weg – er geht über die Laurent-Entwicklung der Funktion f an Stelle z0: |
|
||
|
Residuensatz: G sei ein Gebiet, dessen Rand ∂G eine Summe von einfach-geschlossenen Kurven ist. Die Funktion f sei in G mit höchstens endlich vielen Ausnahmestellen zμ (1≤μ≤n) holomorph und auf ∂G noch stetig, dann gilt: |
|
||
|
Ein Blick zurück als Physiker: Die Funktionentheorie war doch bei vielen physikalischen Gelegenheiten ein elegantes und äußerst nützliches Werkzeug. Die gelben «Behnke Sommer»-Bücher sind mir noch in bester Erinnerung. Der Herr Sommer soll mir in meiner Erinnerung doch in Münster im Schloss über den Weg gelaufen sein, lange ist es her ... |
|||
|
|
Ressourcen
|
Der SciLab-Quellcode (zip) - ausführbar mit einer SciLab-Installation |
|
|
Literatur
|
Scilab Group
|
|
Manolo Venturin
|
|
Dr. J. Wagner
|
|
Robert Grover Brown, Patrick Y. C. Hwang
|
|
Fritz Reinhardt, Franz Soeder
|
|
|
||
| © 2014 Bernd Ragutt Alle Rechte vorbehalten |

|
letzte Änderung: 9. Oktober 2014 Kruschtkiste |
|
|
||
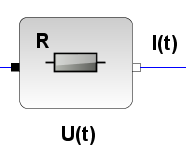
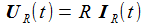
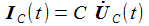
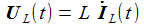
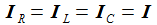
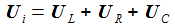
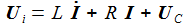
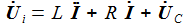
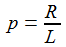
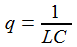
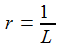
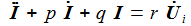
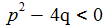
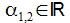
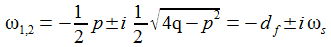
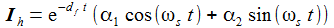
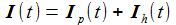
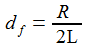
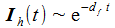
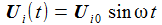
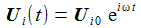
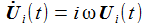
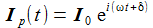
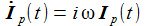
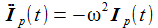
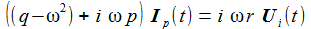
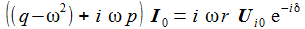
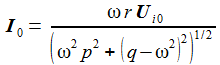
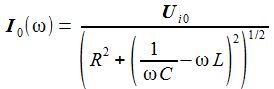
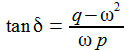
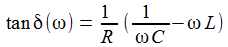
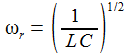
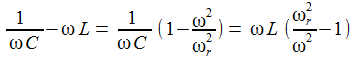
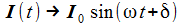
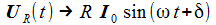
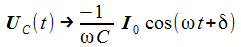
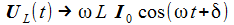
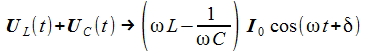
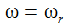
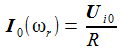
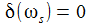
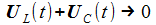
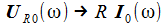
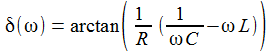
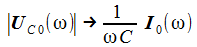
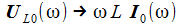
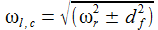
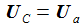
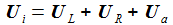
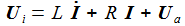
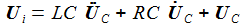
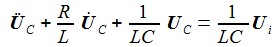
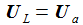
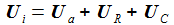
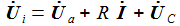
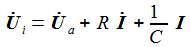
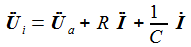
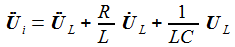
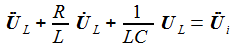
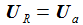
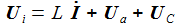
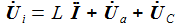
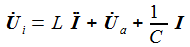
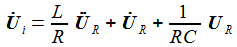
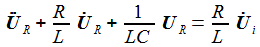
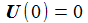
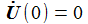
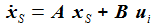
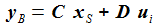
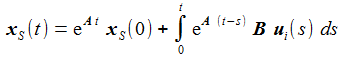
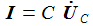
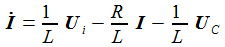
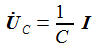
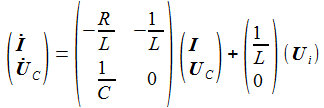
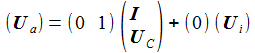
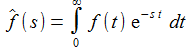
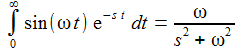
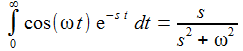
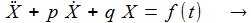
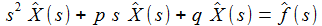
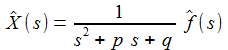
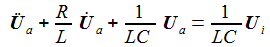
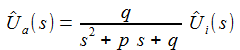
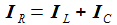
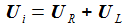
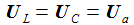
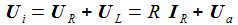
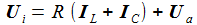
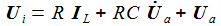
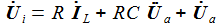
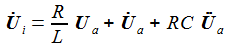
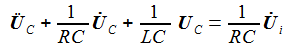
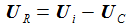
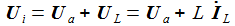
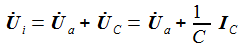
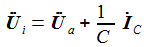
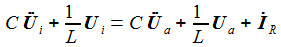
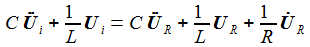
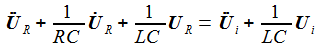
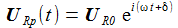
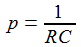
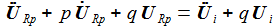
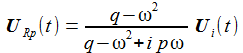
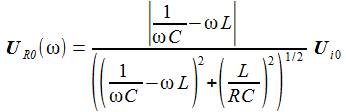
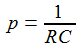
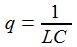
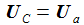
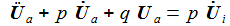
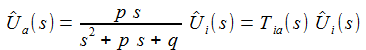
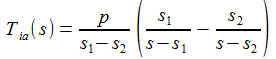
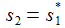
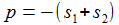
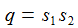
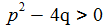
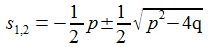
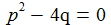
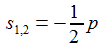
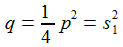
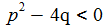
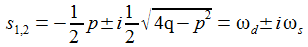
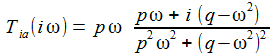
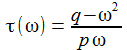
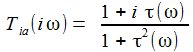
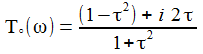
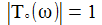
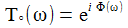
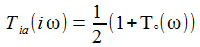
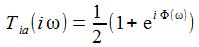
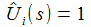
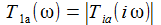
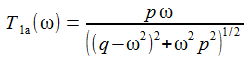
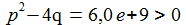
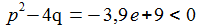
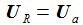
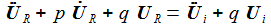
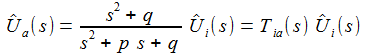
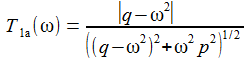
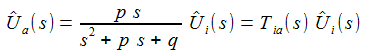
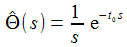
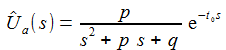
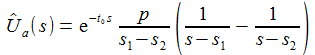
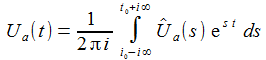
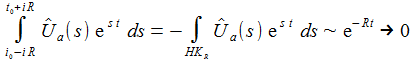
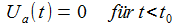
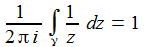
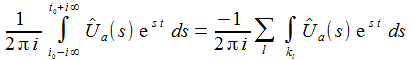
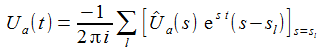
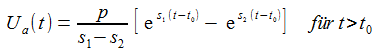
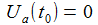
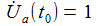
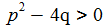
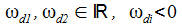
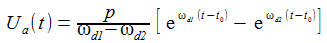
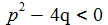
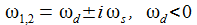
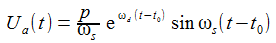
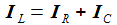
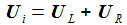
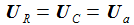
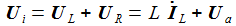
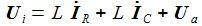
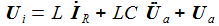
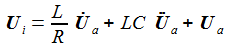
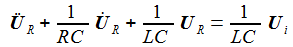
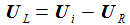
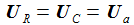
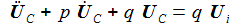
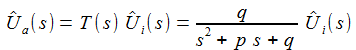
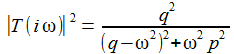
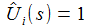 beschreiben.
Die Diagramme zeigen dann auch Spektrum und Phasengang der
Ausgabegröße, wenn man das LCR-Glied mit Weißem Rauschen
füttert.
beschreiben.
Die Diagramme zeigen dann auch Spektrum und Phasengang der
Ausgabegröße, wenn man das LCR-Glied mit Weißem Rauschen
füttert.
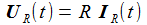
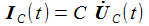
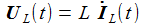
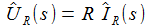
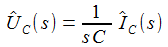
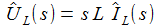
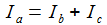
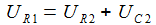
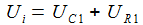
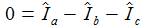
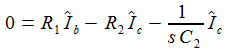
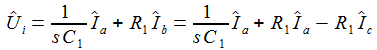
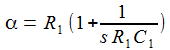
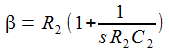
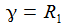
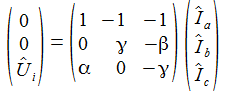
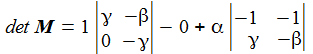
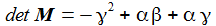
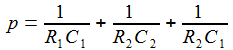
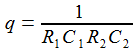

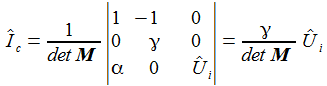
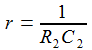
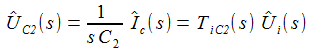
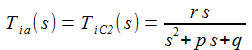

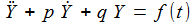
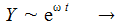
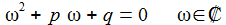
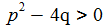
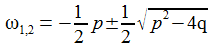
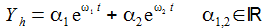
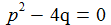
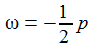
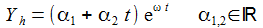
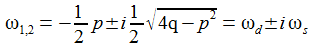
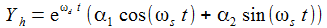
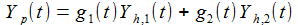
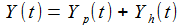
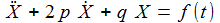
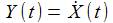 erhält
man die beiden Differentialgleichungen erster Ordnung:
erhält
man die beiden Differentialgleichungen erster Ordnung: