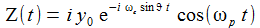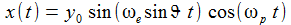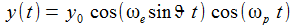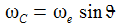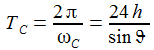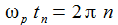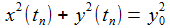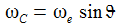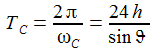|
|
Die Corioliskraft in Näherungslösungen |
|
|
|
|
|
Ein Hinweis: Das unten benutze ENU-Bezugssystem,
|
|
|
Der freie Fall im Schwerefeld
|
Ein Beobachter steht am Breitengrad ϑ und lässt aus der Höhe h einen Ball der Masse m unter dem Einfluss der Schwerkraft senkrecht nach unten fallen. Das Schwerefeld wird als homogen angenommen und die Zentrifugalraft wird vernachlässigt. In welchem Umfang lenkt die Corioliskraft den fallenden Ball aus der Vertikalen? Ich führe ein ENU-Bezugssystem {i=1,2,3} am Breitengrad ϑ ein. Die x1-Achse zeigt nach Osten, die x2-Achse zeigt nach Norden, die vertikale x3-Achse zeigt zum Zenit. |
|
Die Newton'sche Bewegungsgleichung im mitrotierenden Bezugssystem ist gegeben durch: bG ist die durch die Schwerkraft verursachte Beschleunigung, bC die durch die Corioliskraft verursachte. Der konstante Vektor ω beschreibt die Erdrotation in Richtung und Winkelgeschwindigkeit. |
|
|
Die Anfangsbedingungen sind so gewählt - die Anfangsgeschwindigkeit ist also null: |
|
|
In Anbetracht der auftretenden Fallgeschwindigkeiten kann die Corioliskraft als kleine Störkraft betrachtetet werden. |
|
|
Die Lösung für den Geschwindigkeitsvektor in nullter Näherung (also ohne die Coriolisbeschleunigung) ist wohlbekannt: |
|
|
In erster Näherung ergibt sich dann: Neben der vertikalen Bewegung erhält man also eine Beschleunigungskomponente in Richtung Osten. |
|
|
Die Lösung liegt auf der Hand: |
|
|
Die Fallzeit th bis zur Höhe x3=0 ist: |
|
|
Die Auslenkung ΔC für die Fallzeit th durch die Corioliskraft nach Osten ist dann explizit - sie wächst mit der 3. Potenz der Fallzeit: |
|
|
ω = 7,292115 x 10-5 radians/sec g = 9,80616 m/sec² h = 100 m ϑ = 45° |
t100 = 4,516 s ΔC(t100) = 0,0155 m = 1,55 cm |
|
Auf 100 m Fallhöhe bewirkt die Corioliskraft also nur eine recht kleine Ablenkung aus der Vertikalen von 1,55 cm. Am Äquator ist die Auslenkung am größten, am Nordpol gibt es keine solche. Aber: Über lange Wirkungszeiten kann die Corioliskraft durchaus eine gestaltene Wirkung erzielen – so werden die großen Passatwinde auf der Nord- und der Südhalbkugel der Erde durch die Corioliskraft stark in ihrer Strömungsrichtung beeinflusst. |
|
|
|
Das starre Kugelpendel im Schwerefeld
|
Ein Beobachter steht am Breitengrad ϑ und lässt ein Pendel der Länge l und der Masse m unter dem Einfluss der Schwerkraft schwingen. Das Schwerefeld wird als homogen angenommen und die Zentrifugalraft wird vernachlässigt. In welchem Umfang lenkt die Corioliskraft das schwingende Pendel aus der anfänglichen Schwingungebene? Ich führe ein ENU-Bezugssystem {i=1,2,3} am Breitengrad ϑ ein. Der Aufhängepunkt des Pendels ist der Koordinatenursprung. Die x1-Achse zeigt nach Osten, die x2-Achse zeigt nach Norden, die vertikale x3-Achse zeigt zum Zenit. |
|
Ich führe im ENU-Bezugssystem {i=1,2,3} an der Breite ϑ sphärische Koordinaten γ und χ ein. Die vertikale 3-Achse zeigt zum Zenit, der Winkel γ ist der Auslenkwinkel des Pendels gegenüber der Vertikalen entgegen dem Uhrzeigersinn, der Winkel χ ist der Azimuthwinkel. |
|
|
Die Newton'sche Bewegungsgleichung im mitrotierenden Bezugssystem ist gegeben durch: b'G ist die durch die Schwerkraft verursachte Beschleunigung und bC die durch die Corioliskraft verursachte. Zu beachten ist hier, das die radiale Komponente der Schwerkraft durch das starre Pendelseil (besser: Pendelstange) aufgenommen wir, bG ist der wirksame Anteil der durch die Schwerkraft verursachten Beschleunigung. Der konstante Vektor ωe beschreibt die Erdrotation in Richtung und Winkelgeschwindigkeit. |
|
|
Die kartesischen Koordinaten der Pendelmasse müssen dabei zu allen Zeiten eine Nebenbedingung erfüllen: |
|
|
Ich betrachte nur kleine
Auslenkwinkel γ
, setze also
eine lineare Näherung in γ an,
möchte aber weiter in kartesischen Koordinaten rechnen. In dieser
Näherung
|
|
||
|
Die Anfangsbedingungen sind mit χ=0 so gewählt: |
|
||
|
|
|
||
|
Damit erhält man die wirksame Schwerkraftbeschleunigung in linearer Näherung in γ zu: |
|
|
Ich setze nun x1 = x, x2 = y, x3 = z und erhalte die Differentalgleichungen mit
|
|
|
Ich führe eine komplexe Größe ein und erhalte für die beiden ersten Gleichungen eine kompakte Darstellung: |
|
|
Ich probiere den Ansatz
|
|
|
Mit
|
|
|
Als Anfangsbedingungen wird gewählt: |
|
|
Ein wenig Rechnerei ergibt angenähert:
Dabei ist
|
|
|
Für eine nichtrotierende Erde ist also x(t)≡0, dreht sich die Erde, so wandert die Schwingungsebene mit der Kreisfrequenz (ωe sinϑ) nach Osten. Die Periodendauer TC ist dann: |
|
|
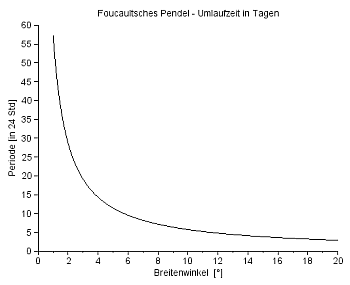
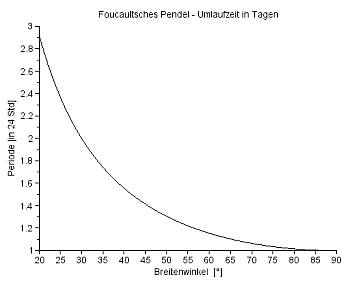
Am Äquator ist ωC=0, das Pendel schwingt also in einer fixen Ebene. Am Pol dreht sich die Schwingungsebene genau einmal in 24 Stunden – oder vom Inertialsystem aus gesehen: das Pendel schwingt in einer fixen Ebene und die Erde dreht sich einmal in 24 Stunden unter dem Pendel hinweg. |
|
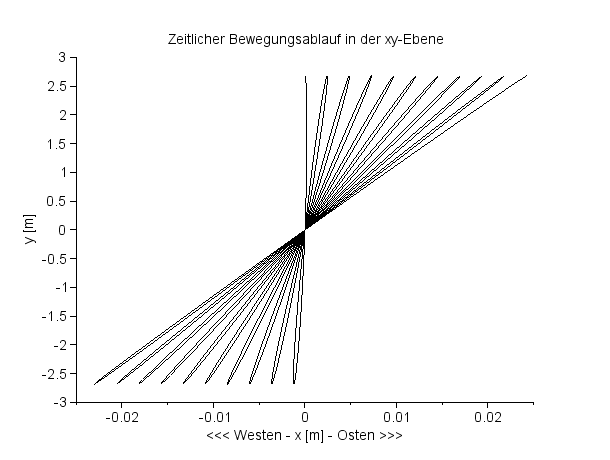
Zeitlicher Bewegungsablauf in der xy-Ebene |
|
|
Das Bild zeigt die ersten 10 Einzelschwingungen. Man beachte die unterschiedlichen Skalierungen der beiden Achsen! Das Pendel hat die Länge 67 m und steht in Paris (Breite 40°); die anfängliche Auslenkung y0 beträgt 1,35 m. |
|
|
Die Endpunkte der Einzelschwingungen werden für die Zeiten tn, n=0,1,2,.. angenommen. Diese Endpunkte liegen auf einem Kreis mit dem Radius y0. Der aktuelle Endpunkt wandert auf diesem Kreis mit der Winkelgeschwindigkeit ωC. Für einen vollständigen Umlauf braucht er die Zeit TC. |
|
|
Am Pol scheint sich die Schwingungsebene des Pendels einmal in 24 Stunden zu drehen, zum Äquator hin dauert ein voller Umlauf immer länger, am Äquator tut sich nichts mehr (TC=∞) ... |
|
|
Pendel-Umlaufzeiten - Breiten 1° - 20° |
|
|
Pendel-Umlaufzeiten - Breiten 20° - 90° |
|
|
|
Wirbelnde Wasser im Waschbecken
|
Fließt Wasser aus einem Waschbecken ab, so bildet sich im Abflusstrichter ein spiralförmiger Wasserstrudel, der linksherum oder rechtsherum wirbeln kann. Der Grund: Das Abflussrohr ist eng, das nachfließende Wasser muss seitlich horizontal ausweichen, es bildet sich ein Spiralwirbel. Wie herum das Wasser nun abfließt, hängt von der Beckenform und vom Abfluss ab, die Corioliskraft hat sicher keinen Einfluss auf dieses Geschehen. Es ist wie bei den Verschwörungstheorien, der größte Unfug hat auch die höchste Beständigkeit – oder auch: eine abstruse Erklärung ist immer noch besser als gar keine. |
|
|
Dazu denn doch eine kleine quantitative Betrachtung am Nordpol. ω ist die Winkelgeschwindigkeit der Erdrotation. v⊥ ist die Horizontalgeschwindigkeit irgendeines schnell dahin fließenden Wassertropfens. Die Corioliskraft bc hat die Größe: |
bC(θ=½ π) = 2 ω v⊥
ω ≈ 2π/(24⋅60⋅60) 1/s v⊥ ≈ 1,5 m/s |
|
Zum Größenvergleich, bG ist die Gravitationsbeschleunigung, sie wirkt zwar nur in der vertikalen, ist aber die erste Referenzgröße: |
bC = 2,2 10-4 m/s2 bG = 9,8 m/s2 |
|
Zwischen den beiden Beschleunigungen liegen also fast 5 Größenordnungen. Zudem liegt der Betrachtungszeitraum bei einigen Sekunden – solch kleinen Kräfte könnten hier nur über große Zeiträume Wirkung zeigen. Dennoch wäre eine Abschätzung von weiteren wirksamen Horizontalkräften eine nette Angelegenheit ... |
|
|
|
||
| © 2014 Bernd Ragutt
Alle Rechte vorbehalten |

|
letzte Änderung: 28. Mai 2016 Kruschtkiste |
|
|
||
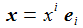
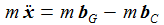
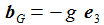
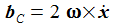
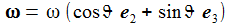
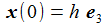
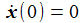
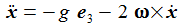
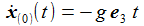
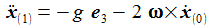
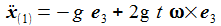
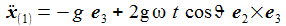
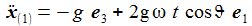
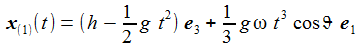
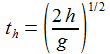
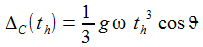
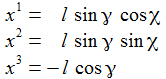
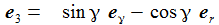
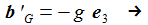
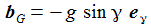
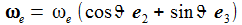
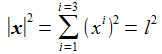
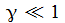 erhalte ich dann:
erhalte ich dann:
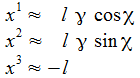
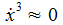
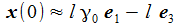
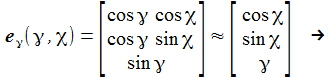
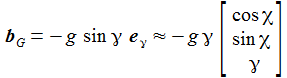
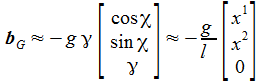
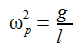
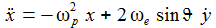
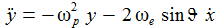
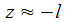
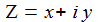
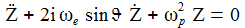
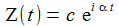 und
erhalte eine quadratische Gleichung in α
mit den Lösungen:
und
erhalte eine quadratische Gleichung in α
mit den Lösungen:
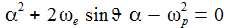
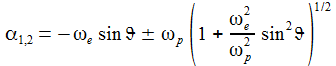
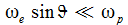 erhält
man die genäherten Lösungen für α1,2
und dann die allgemeine Lösung für Z
mit komplexen Konstanten c1,2:
erhält
man die genäherten Lösungen für α1,2
und dann die allgemeine Lösung für Z
mit komplexen Konstanten c1,2:
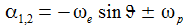
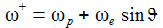
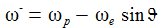
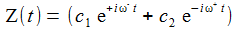
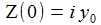
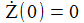
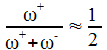 ,
etc.
,
etc.