Inhalt
| Prolog | Vollvenus, Sichelvenus? Neuvenus? |
| Einstieg | Welche Planeten zeigen denn Phasen? |
| Innensicht Außensicht | |
| Modell! | Wie könnte man das Problem angehen? |
| Gitter Farbe Verläufe Tabelle Rotation | |
| Welt | Was noch fehlt? - Die reale Welt! |
| Resultat | Und so sieht das Ergebnis aus ... |
| CelestLab Stellarium | |
| Danke | Hat Spaß gemacht! |
| Dinge | Quellcode zum Ausprobieren |
Prolog
Vollvenus, Sichelvenus? Oder auch die Neuvenus?
Das unser Erdtrabant sich als Neumond fast unsichtbar machen kann, ist wohlbekannt, nicht zu übersehen und auch leicht alle vier Wochen zu beobachten. Daß an unserem Himmel auch Planeten ein Leben in Phasen führen, ist nicht so offensichtlich.
Die Werkzeugkomponente CelestLab innerhalb der wissenschaftlichen Werkbank SciLab bringt ein Demo-Programm 'Mondphasen' mit sich, dass ich ausbauen möchte, um die Phasen des Planeten Venus ausgeben zu können.
Einstieg
Welche Planeten zeigen einen Phasenablauf?
Die von der Sonne beschienene Seite der Venus nenne ich Vorderseite. Schon eine schnelle Skizze zeigt, dass wir auf der Erde die Venus nicht nur von vorne sondern auch von der Seite betrachten können.
Wir auf der Erde werden also Licht und Schatten auf der Venus sehen: ihre Phasen eben.
Innensicht
Sonne, Venus und Erde sollen nun für eine kleine Rechnerei in einer Ebene kreisen, die Erde kreist außen, die Venus innen.
Der Winkel Φ zwischen der Lichtachse Sonne - Venus und der Sichtachse Erde - Venus bestimmt, wie wir die Venus sehen.
Hat dieser Winkel den Wert 0 oder π (pi), so liegen die drei Himmelskörper auf einer Geraden, im Prinzip hätten wir dann Vollvenus oder Neuvenus - wenn nicht die helle Sonne die Venus überstrahlen würde.
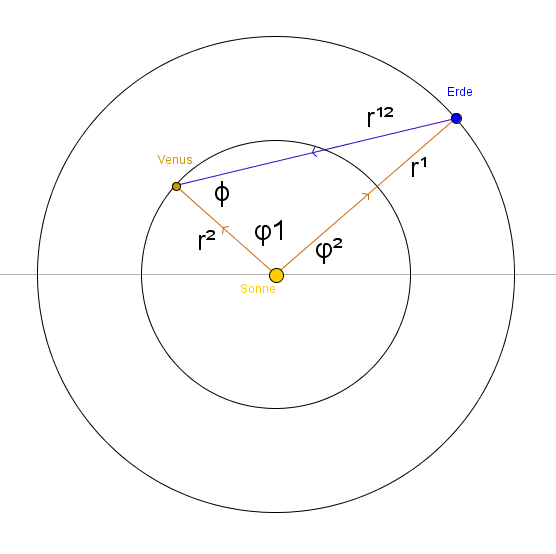
Sonne, Venus und Erde in einer Ebene
| Die beiden Vektoren r1 und r2 gehen jeweils von der Sonne zur Venus und zur Erde. Der Vektor r12 geht von der Erde zur Sonne. | |
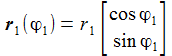
|
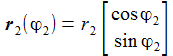
|
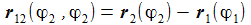
|
|
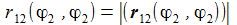
|
|
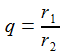
|
|
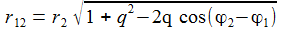
|
|
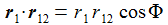
|
|
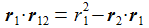
|
|
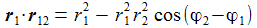
|
|
| Damit hat man eine Gleichung für den Winkel Φ in Abhängigkeit von der Stellung der beiden Planeten. | |
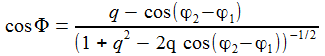
|
|
Man kann ohne Weiteres den Azimuthwinkel für die Erde gleich null setzen und erhält dann den dargestellten Kurvenverlauf für Φ in Abhängigkeit vom Venuswinkel φ1.
Das Verhältnis der Radien für Venus und Erde ist q=0,72.
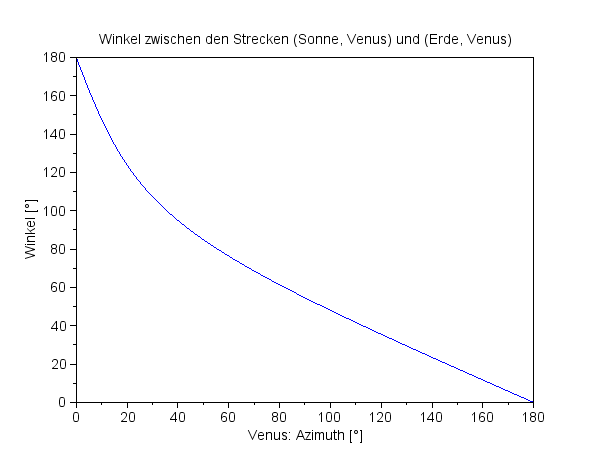
Venus: Der Verlauf des Winkels Φ
zwischen Licht- und Sichtachse
"Mit Hilfe eines Teleskops kann man erkennen, dass die Venus Phasen hat, ähnlich wie der Mond. Als volle Scheibe ist sie am kleinsten, weil sie dann – von der Erde aus gesehen – hinter der Sonne steht, also am weitesten von uns entfernt ist. Die Venus hat bei zunehmender Phase ihre maximale Helligkeit und dabei die Größenklasse -4,4; sie ist dann 15-mal heller als der hellste Fixstern. Die Phasen und Positionen der Venus am Himmel wiederholen sich mit einer ... Periode von 1,6 Jahren." Microsoft Encarta 2002
Außensicht
Und wie sieht das Bild nun für äußere Planeten, etwa für den Mars, aus? Es ist ein leichtes die obige Rechnung für den Mars zu wiederholen, hier sei gleich das Ergebnis aufgezeigt.
Die Größe q ist nun der Quotient aus dem Erdradius und dem Radius des äußeren Planeten, ist also kleiner als Eins.
Das Verhältnis der Radien für Erde und Mars ist q=0,66. Für kleine q geht der Winkel Φ gegen null, man kann dem weit entfernten, äußeren Planeten nicht in die Flanke schauen. Und für den Mars, der ja nicht so weit weg ist, wie sieht es da aus?
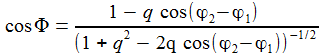
|
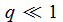
|
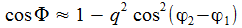
|
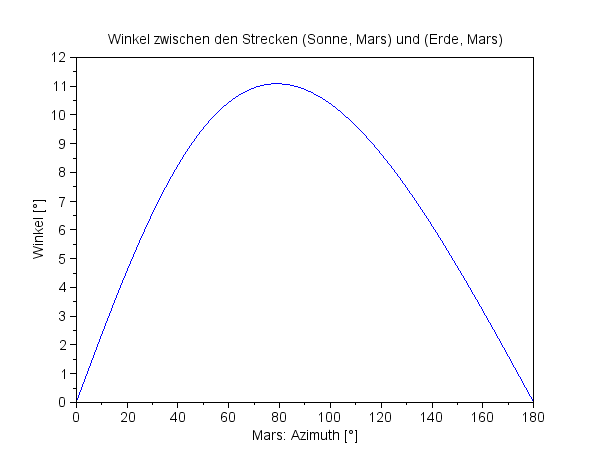
Mars: Der Verlauf des Winkels Φ
zwischen Licht- und Sichtachse
Der Winkels Φ wird also höchstens 11° groß, nämlich wenn Sonne, Mars und Erde einen rechten Winkel bilden - 11° ist wohl ein zu kleiner Wert, um zu einem Phasenverlauf zu führen, der auf der Erde dem bloßen Auge auffallen würde.
Modell
Wie könnte man das Problem denn nun angehen?
Als ich mir die ClestLab-Demo "Moon Phases" zum ersten Mal anschaute, begann der Physikerkopf natürlich sofort nach Lösungswegen zu suchen. Dass, was ein Beobachter auf der Erde vom Mond oder von der Venus sieht, müsste als Schnittmenge zweier Halbkugeln zu beschreiben sein, oder?
Aber bitte zuerst den SciLab-Quellcode des Herrn "Auteur: A. Lamy" anschauen! Wie hat er das Problem angegangen: Er hat keinen Algorithmus auf die Beine gestellt, sondern ein Modell gebaut.
Zudem: Die SciLab-Skriptsprache ist doch etwas Anderes als eine gewöhnliche Programmiersprache. Ein wenig Quellcode-Studium hilft einem doch mächtig auf die Sprünge.
Gitterdraht
Ein dreidimensionales Drahtgittermodell für die Kugel muss her!
Ich orientiere mich hier an der CelestLab-Demo, habe aber auch ein wenig experimentiert, um zu verstehen, was in der Demo wie abläuft.

Die Funktion fShereData gibt drei Vektoren der Länge 101 zurück, die die Koordinaten einer Kugel beschreiben, anschließend wird diese Funktion aufgerufen und das Ergebnis mit plot3d2 graphisch ausgegeben. Wunderschön kompakt der Code, da die Operationen als Vektoroperationen ausgeführt werden. Das Ergebnis sieht so aus:

Die Kugel als Gittergeflecht
Farbe
Damit man die Kacheln des Gittermodel besser erkennt, kann man sie mit einem kleinen Algorithmus '10*(fcData.z)+1' einfärben - das Ganze ist wieder vektoriell zu verstehen:


Die Kugel als Gittergeflecht - eingefärbt
Verläufe
Die Venus oder der Mond hat eine helle gelbe und eine dunkle graue Seite. Ich benötige also zwei Grundfarben gelb und grau und Farbverläufe für einen natürlichen Farbübergang. 63 Farben werden spendiert, über die mit Farbindizes zugegriffen wird.
Die Funktion setColor nimmt die Verteilung der Farben entsprechend dem Einstrahlwinkels des Lichts auf die Kachel vor. Der Funktion wird ein Vektor mit dem cosinus des Einstrahlwinkels des Lichts und ein Vektor mit den 63 Farbindizes übergeben.
Das erste find im Quellcode unten findet alle Indizes, für die der cosinus des Einstrahlwinkels kleiner oder gleich als -0,03 ist. Im Farbvektor col, der von setColor zurückgegeben wird, erhält der Teilvektor col(I) die erste Farbe grau zugewiesen.
Beim zweiten find wird der schmale Übergangsbereich von grau nach gelb abgehandelt.
Beim dritten find wird ein Farbverlauf von einem dunklen Gelb zu einem hellen Gelb definiert.

Um die Berechnung einfach zu gestalten, wird hierfür ein Bezugssystem gewählt, in dem die Sonne und der beleuchtete Himmelskörper auf der z-Achse liegen.
Die Kacheln werden mit der cosinus-Funktion cos(Θ) eingefärbt, es ist ja cos(0)=1, da wird das helle Gelb genommen und bei einem Winkel, für den cos(Θ)=0,03 gilt, wird das dunkle Gelb verwendet.
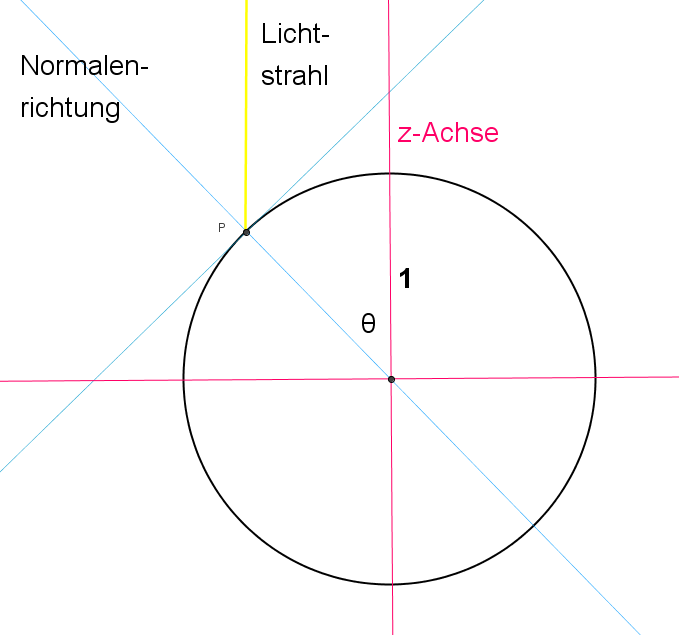
Kugeleinfärbung

Zwei (falsch-)farbige Halbkugeln mit einem Übergangsbereich
Farbtabelle
Die Farben stimmen noch nicht, es muss noch die richtige Farbtabelle gesetzt werden. p ist ein Vektor mit 31 Werten äquidistanten Werten zwischen 0 und 30. CL_dMult ist die komponentenweise Multiplikation.
Für die beiden Farbtabellen Cmap1 und Cmap2 wird jeweils zwischen den Grenzwerten c0 und c1, beziehungsweise c1 und c2 interpoliert.


Das sieht doch bestens aus!
Rotation
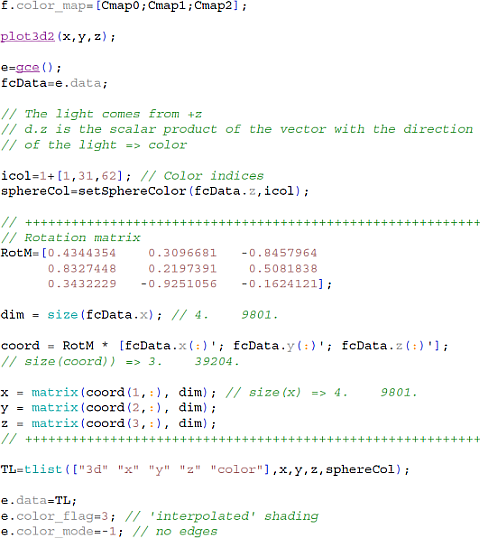
Wir haben eine wunschgemäß eingefärbte Kugel - in drei Dimensionen natürlich. Wir können nun sozusagen um die Kugel herum gehen und könnten so Venusphasen betrachten.
Oder wir unterwerfen die eingefärbten Kacheln des Gittermodells einer Rotation. Wir drehen die beleuchtete Kugel auf den Beobachter zu, der Rotationswinkel ist offensichtlich, es ist der Winkel zwischen Licht- und Sichtachse.
Im Testbeispiel ist diese Rotationsmatrix fest und heißt im Quellcode unten rotM. Die Kacheldaten werden mit fcData)=e.data aus dem mit plot3d2 erzeugten Grafik-Objeckt ausgelesen.
Jede der 9801 Kacheln wird durch 4 Punkte definiert, also durch insgesamt 4x3=12 Koordinaten. Die Größe fcData.x ist hier eine Datenstruktur, die aus 9801 Spalten zu je 4 x-Koordinaten für je eine Kachel besteht. Das Hochkomma ' erzeugt die transponierte Größe, fcData.x(:)' sind dann 9801 Zeilen mit je 4 x-Koordinaten.
Die Größe [1;2;3] definiert in SciLab einen Spaltenvektor, [fcData.x(:)'; fcData.y(:)'; fcData.z(:)'] ergeben dann einen Multivektor, das sind 39204 Spaltenvektoren mit den x-, y- und z-Komponenten der Kacheln. Die Matrix-Multiplikation mit RotM iteriert über den Multivektor und erzeugt 39204 transformierte Vektoren.
Mittels der matrix-Operation wird die Ausgangsstruktur x, y und z zurück gewonnen, die nun wieder in das Grafikobjeckt geschreiben werden kann.
Und das Result sieht schließlich wie gewünscht aus! Famos.

Fast ein Halbmond
Welt
Was noch fehlt? - Die Anbindung an die reale Welt
Ein Modell haben wir für unseren Zweck und der Weg zur Sichel ist eine Rotation. Wir brauchen noch die Himmelspositionen von Sonne und Venus zum Beobachtungszeitpunkt und müssen diese Positionen zum Standort des Beobachters in Bezug setzen.
Hier ein Ausschnitt aus einem kommentierten Testprogramm zur Sache. M' ist die zu M inverse Matrix. Die CelestLab-Routine CL_rot_defFrameVec erzeugt aus den Argumenten ein Dreibein und gibt die zugeordnete Rotationsmatrix zurück.
Der Ursprungscode der CelestLab-Demo sieht etwas anders auf. Per Augenschein decken sich die Ergebnisse.

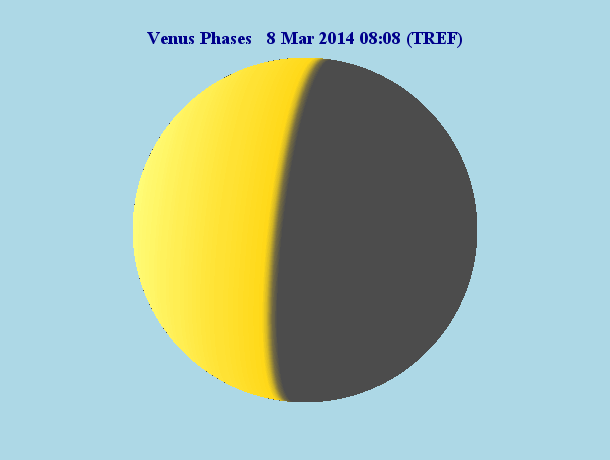
Resultat
Und so sieht das schlussendliche Ergebnis aus ...
... und zwar am Sonnabend, den 8. März 2014 um kurz nach 9 Uhr (Winterzeit).
Als Testwerkzeug verwende ich das frei verfügbare Stellarium. Der Himmel ist als Nachthimmel eingestellt.
Ein Blick noch auf das Paar Sonne und Venus - mit dem Merkur dazwischen - in einer perspektivischen Projektion, hier bildet der Horizont eine gerade Linie: das Bild ist stimmig.
Sonne und Venus am frühen Morgen - stimmig!
Danke
Hat Spaß gemacht!
Ein Dankeschön an die Ersteller von CelestLab!!
Ressourcen
Der SciLab-Quellcode (zip) - ausführbar mit einer SciLab-Installation
Der SciLab-Quellcode (pdf) - als pdf-Datei zum Anschauen